ƒøƒ⁄»ð
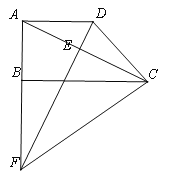
°æƒø°ø ˝—ß≤ªΩˆ «“ª√≈—ßø∆£¨“≤ «“ª÷÷ŒƒªØ£¨º¥ ˝—ߌƒªØ. ˝—ߌƒªØ∞¸¿® ˝—ß ∑°¢ ˝—ß√¿∫Õ ˝—ß”¶”√µ»∂ý∑Ω√Ê.π≈ ±∫Ú£¨‘⁄ƒ≥∏ˆÕıπ˙¿Ô”–“ªŒª¥œ√˜µƒ¥Û≥º£¨À˚∑¢√˜¡Àπ˙º œÛ∆£¨œ◊∏¯¡Àπ˙Õı£¨π˙Õı¥”¥À√‘…œ¡Àœ¬∆£¨Œ™¡À∂‘¥œ√˜µƒ¥Û≥º±Ì æ∏––ª£¨π˙Õı¥”¶¬˙◊„’‚Œª¥Û≥ºµƒ“ª∏ˆ“™«Û.¥Û≥ºÀµ£∫°∞æÕ‘⁄’‚∏ˆ∆Â≈Ã…œ∑≈“ª–©√◊¡£∞….µ⁄![]() ∏Ò∑≈
∏Ò∑≈![]() ¡£√◊£¨µ⁄
¡£√◊£¨µ⁄![]() ∏Ò∑≈
∏Ò∑≈![]() ¡£√◊£¨µ⁄
¡£√◊£¨µ⁄![]() ∏Ò∑≈
∏Ò∑≈![]() ¡£√◊£¨»ª∫Û «
¡£√◊£¨»ª∫Û «![]() ¡£°¢
¡£°¢![]() ¡£°¢
¡£°¢![]() ¡£°§°§°§°§°§°§“ª÷ªµΩµ⁄
¡£°§°§°§°§°§°§“ª÷ªµΩµ⁄![]() ∏Ò.°±°∞ƒ„’Ê…µ£°æÕ“™’‚√¥“ªµ„√◊¡££ø°±π˙Õıπ˛π˛¥Û–¶.¥Û≥ºÀµ£∫°∞æÕ≈¬ƒ˙µƒπ˙ø‚¿Ô√ª”–’‚√¥∂ý√◊£°°±π˙Õıµƒπ˙ø‚¿Ô’Ê√ª”–’‚√¥∂ý√◊¬£øÂ÷–Œ ÂæÕ ««Û
∏Ò.°±°∞ƒ„’Ê…µ£°æÕ“™’‚√¥“ªµ„√◊¡££ø°±π˙Õıπ˛π˛¥Û–¶.¥Û≥ºÀµ£∫°∞æÕ≈¬ƒ˙µƒπ˙ø‚¿Ô√ª”–’‚√¥∂ý√◊£°°±π˙Õıµƒπ˙ø‚¿Ô’Ê√ª”–’‚√¥∂ý√◊¬£øÂ÷–Œ ÂæÕ ««Û![]() «∂ý…Ÿ£ø«ÎÕ¨—ß√«‘ƒ∂¡“‘œ¬Ω‚¥π˝≥ÃæÕ÷™µ¿¥∞∏¡À.
«∂ý…Ÿ£ø«ÎÕ¨—ß√«‘ƒ∂¡“‘œ¬Ω‚¥π˝≥ÃæÕ÷™µ¿¥∞∏¡À.
…Ë![]() ,
,
‘Ú![]()
![]()
![]()
º¥£∫![]()
¬ µ…œ£¨∞¥’’’‚Œª¥Û≥ºµƒ“™«Û£¨∑≈¬˙“ª∏ˆ∆Â≈Ã…œµƒ![]() ∏ˆ∏Ò◊”–Ë“™
∏ˆ∏Ò◊”–Ë“™![]() ¡£√◊.ƒ«√¥
¡£√◊.ƒ«√¥![]() µΩµ◊∂ý¥Ûƒÿ?ΩË÷˙º∆À„ª˙÷–µƒº∆À„∆˜Ω¯––º∆À„£¨ø…÷™¥∞∏ «“ª∏ˆ
µΩµ◊∂ý¥Ûƒÿ?ΩË÷˙º∆À„ª˙÷–µƒº∆À„∆˜Ω¯––º∆À„£¨ø…÷™¥∞∏ «“ª∏ˆ![]() Œª ˝:
Œª ˝:![]()
![]() £¨’‚ «“ª∏ˆ∑«≥£¥Ûµƒ ˝£¨À˘“‘π˙Õı «≤ªƒÐ¬˙◊„¥Û≥ºµƒ“™«Û.«Î”√ƒ„—ßµΩµƒ∑Ω∑®Ω‚戓‘œ¬Œ Â:
£¨’‚ «“ª∏ˆ∑«≥£¥Ûµƒ ˝£¨À˘“‘π˙Õı «≤ªƒÐ¬˙◊„¥Û≥ºµƒ“™«Û.«Î”√ƒ„—ßµΩµƒ∑Ω∑®Ω‚戓‘œ¬Œ Â:
![]() Œ“π˙π≈¥˙ ˝—ß√˚÷¯°∂À„∑®Õ≥◊⁄°∑÷–”–»Áœ¬Œ Â:°∞‘∂Õ˚Œ°Œ°À˛∆þ≤„£¨∫Ïπ‚µ„µ„±∂º”‘ˆ£¨π≤µ∆»˝∞Ÿ∞À Æ“ª£¨«ÎŒ º‚Õ∑º∏’µµ∆?°±“‚Àº «:“ª◊˘
Œ“π˙π≈¥˙ ˝—ß√˚÷¯°∂À„∑®Õ≥◊⁄°∑÷–”–»Áœ¬Œ Â:°∞‘∂Õ˚Œ°Œ°À˛∆þ≤„£¨∫Ïπ‚µ„µ„±∂º”‘ˆ£¨π≤µ∆»˝∞Ÿ∞À Æ“ª£¨«ÎŒ º‚Õ∑º∏’µµ∆?°±“‚Àº «:“ª◊˘![]() ≤„À˛π≤π“¡À
≤„À˛π≤π“¡À![]() ’µµ∆£¨«“œý¡⁄¡Ω≤„÷–µƒœ¬“ª≤„µ∆ ˝ «…œ“ª≤„µ∆ ˝µƒ
’µµ∆£¨«“œý¡⁄¡Ω≤„÷–µƒœ¬“ª≤„µ∆ ˝ «…œ“ª≤„µ∆ ˝µƒ![]() ±∂£¨‘ÚÀ˛µƒ∂•≤„π≤”–∂ý…Ÿ’µµ∆?
±∂£¨‘ÚÀ˛µƒ∂•≤„π≤”–∂ý…Ÿ’µµ∆?
![]() º∆À„:
º∆À„: ![]()
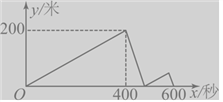
![]() ƒ≥÷–—ß°∞ ˝—ß…ÁÕ≈°±ø™∑¢¡À“ªøÓ”¶”√»Ìº˛£¨Õ∆≥ˆ¡À°∞Ω‚ ˝—ߪһ°»Ìº˛º§ªÓ¬Î°±µƒªÓ∂Ø.’‚øӻ̺˛µƒº§ªÓ¬ÎŒ™œ¬√Ê ˝—ߌ µƒ¥∞∏£∫
ƒ≥÷–—ß°∞ ˝—ß…ÁÕ≈°±ø™∑¢¡À“ªøÓ”¶”√»Ìº˛£¨Õ∆≥ˆ¡À°∞Ω‚ ˝—ߪһ°»Ìº˛º§ªÓ¬Î°±µƒªÓ∂Ø.’‚øӻ̺˛µƒº§ªÓ¬ÎŒ™œ¬√Ê ˝—ߌ µƒ¥∞∏£∫
“—÷™“ª¡– ˝£∫![]() £¨∆‰÷–µ⁄“ªœÓ «
£¨∆‰÷–µ⁄“ªœÓ «![]() £¨Ω”œ¬¿¥µƒ¡ΩœÓ «
£¨Ω”œ¬¿¥µƒ¡ΩœÓ «![]() £¨‘ŸΩ”œ¬¿¥µƒ»˝œÓ «
£¨‘ŸΩ”œ¬¿¥µƒ»˝œÓ «![]() £¨“‘¥À¿ýÕ∆£¨«Û¬˙◊„»Áœ¬Ãıº˛µƒÀ˘”–’˝’˚ ˝
£¨“‘¥À¿ýÕ∆£¨«Û¬˙◊„»Áœ¬Ãıº˛µƒÀ˘”–’˝’˚ ˝![]() £¨«“’‚“ª ˝¡–«∞
£¨«“’‚“ª ˝¡–«∞![]() œÓ∫ÕŒ™
œÓ∫ÕŒ™![]() µƒ’˝’˚ ˝√ð.«Î÷±Ω”–¥≥ˆÀ˘”–¬˙◊„Ãıº˛µƒ»Ìº˛º§ªÓ¬Î’˝’˚ ˝
µƒ’˝’˚ ˝√ð.«Î÷±Ω”–¥≥ˆÀ˘”–¬˙◊„Ãıº˛µƒ»Ìº˛º§ªÓ¬Î’˝’˚ ˝![]() µƒ÷µ.
µƒ÷µ.
°æ¥∞∏°ø£®1£©3£ª£®2£©![]() £ª£®3£©
£ª£®3£©![]()
°æΩ‚Œˆ°ø
![]() …ËÀ˛µƒ∂•≤„π≤”–
…ËÀ˛µƒ∂•≤„π≤”–![]() ’µµ∆£¨∏˘æð“‚¡–≥ˆ∑Ω≥ã¨Ω¯––Ω‚¥º¥ø….
’µµ∆£¨∏˘æð“‚¡–≥ˆ∑Ω≥ã¨Ω¯––Ω‚¥º¥ø….
![]() ≤Œ’’ƒø÷–µƒΩ‚Â∑Ω∑®Ω¯––º∆À„º¥ø….
≤Œ’’ƒø÷–µƒΩ‚Â∑Ω∑®Ω¯––º∆À„º¥ø….
![]() ”…“‚«Ûµ√ ˝¡–µƒ√ø“ªœÓ£¨º∞«∞nœÓ∫ÕSn=2n+1-2-n£¨º∞œÓ ˝£¨”…“‚ø…÷™£∫2n+1Œ™2µƒ’˚ ˝√ð£Æ÷ª–ËΩ´-2-nœ˚»•º¥ø…£¨∑÷±∑÷±º¥ø…«Ûµ√Nµƒ÷µ
”…“‚«Ûµ√ ˝¡–µƒ√ø“ªœÓ£¨º∞«∞nœÓ∫ÕSn=2n+1-2-n£¨º∞œÓ ˝£¨”…“‚ø…÷™£∫2n+1Œ™2µƒ’˚ ˝√ð£Æ÷ª–ËΩ´-2-nœ˚»•º¥ø…£¨∑÷±∑÷±º¥ø…«Ûµ√Nµƒ÷µ
![]() …ËÀ˛µƒ∂•≤„π≤”–
…ËÀ˛µƒ∂•≤„π≤”–![]() ’µµ∆£¨”…“‚µ√
’µµ∆£¨”…“‚µ√
![]() .
.
Ω‚µ√![]() £¨
£¨
![]() ∂•≤„π≤”–
∂•≤„π≤”–![]() ’µµ∆.
’µµ∆.
![]() …Ë
…Ë![]() ,
,
![]()
![]() ,
,
º¥£∫![]()
![]() .
.
º¥![]()
![]() ”…“‚ø…÷™£∫20µ⁄“ªœÓ,20,21µ⁄∂˛œÓ,20,21,22µ⁄»˝œÓ,°≠20,21,22°≠,2n1µ⁄nœÓ£¨
”…“‚ø…÷™£∫20µ⁄“ªœÓ,20,21µ⁄∂˛œÓ,20,21,22µ⁄»˝œÓ,°≠20,21,22°≠,2n1µ⁄nœÓ£¨
∏˘æðµ»±» ˝¡–«∞nœÓ∫Õπ´ Ω,«Ûµ√√øœÓ∫Õ∑÷±Œ™£∫![]()
√øœÓ∫¨”–µƒœÓ ˝Œ™£∫1£¨2£¨3£¨°≠£¨n£¨
◊Ðπ≤µƒœÓ ˝Œ™![]()
À˘”–œÓ ˝µƒ∫ÕŒ™![]()
![]()
![]()
![]()
”…“‚ø…÷™£∫![]() Œ™2µƒ’˚ ˝√ð£¨÷ª–ËΩ´2nœ˚»•º¥ø…£¨
Œ™2µƒ’˚ ˝√ð£¨÷ª–ËΩ´2nœ˚»•º¥ø…£¨
‘Ú¢Ÿ1+2+(2n)=0,Ω‚µ√£∫n=1,◊Ðπ≤”–![]() £¨≤ª¬˙◊„N>10£¨
£¨≤ª¬˙◊„N>10£¨
¢⁄1+2+4+(2n)=0,Ω‚µ√£∫n=5,◊Ðπ≤”–![]() ¬˙◊„
¬˙◊„![]() £¨
£¨
¢€1+2+4+8+(2n)=0,Ω‚µ√£∫n=13,◊Ðπ≤”–![]() ¬˙◊„
¬˙◊„![]() £¨
£¨
¢Ð1+2+4+8+16+(2n)=0,Ω‚µ√£∫n=29,◊Ðπ≤”–![]() ≤ª¬˙◊„
≤ª¬˙◊„![]() £¨
£¨
°ý![]()

 ◊¥‘™∑ª»´≥ÃÕª∆∆µº¡∑≤‚œµ¡–¥∞∏
◊¥‘™∑ª»´≥ÃÕª∆∆µº¡∑≤‚œµ¡–¥∞∏ ÷±Õ®πÛ÷ð√˚–£÷Ð≤‚‘¬øº÷±Õ®√˚–£œµ¡–¥∞∏
÷±Õ®πÛ÷ð√˚–£÷Ð≤‚‘¬øº÷±Õ®√˚–£œµ¡–¥∞∏