题目内容
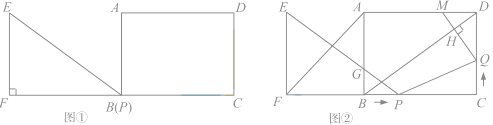
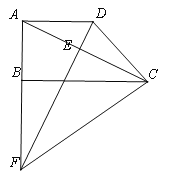
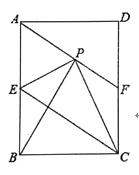
【题目】如图,在矩形ABCD中,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,联结AP并延长AP交CD于F点,
(1)求证:四边形AECF为平行四边形;
(2)如果PA=PC,联结BP,求证:△APB![]() △EPC.
△EPC.
【答案】(1)见解析;(2)见解析.
【解析】
(1)由折叠的性质得到EC垂直平分BP,根据E为AB中点,得到AE=EB,根据EQ为△ABP的中位线,得出AF∥EC即可;
(2)由翻折性质∠EPC=∠EBC=,∠PEC=∠BEC,再求出△AEP为等边三角形即可求解.
解:(1)证明:由折叠得到EC垂直平分BP,
设EC与BP交于Q,∴BQ=EQ
∵E为AB的中点, ∴AE=EB,
∴EQ为△ABP的中位线,∴AF∥EC,
∵AE∥FC, ∴四边形AECF为平行四边形;
(2)∵AF∥EC,∴∠APB=∠EQB=90°
由翻折性质∠EPC=∠EBC=90°,∠PEC=∠BEC
∵E为直角△APB斜边AB的中点,且AP=EP,
∴△AEP为等边三角形 , ∠BAP=∠AEP=60°,
![]()
在△ABP和△EPC中, ∠BAP=∠CEP,∠APB=∠EPC,AP=EP
∴△ABP≌△EPC(AAS),

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目