题目内容
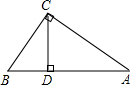
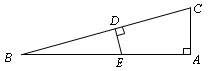
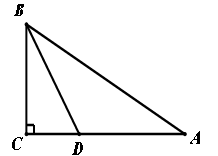
如图，△ABC中，∠A=90°，∠C=75°，AC=6，DE垂直平分BC，则BE= ．
12．
试题分析：根据三角形的内角和求出∠B=15°，再根据垂直平分线的性质求出BE=EC，∠1=∠B=15°，然后解直角三角形计算．
试题解析：如图：
∵△ABC中，∠A=90°，∠C=75°，
∴∠B=15°
连接EC
∵DE垂直平分BC
∴BE=EC，∠1=∠B=15°
∴∠2=∠ACB-∠1=75°-15°=60°
在Rt△ACE中，∠2=60°，∠A=90°
∴∠3=180°-∠2-∠A=180°-60°-90°=30°
故EC=2AC=2×6=12，
即BE=12．
练习册系列答案
中考解读考点精练系列答案
相关题目
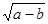+|a?3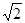
|＝0．C为AB的中点，P是线段AB上一动点，D是x轴正半轴上一点，且PO=PD，DE⊥AB于E．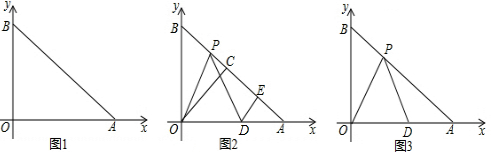
.由此可知新正方形边长等于两个小正方形组成的矩形的对角线长．
