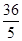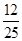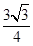题目内容
某园艺公司对一块直角三角形的花园进行改造,测得两直角边长分别为a=6米,b=8米.现要将其扩建成等腰三角形,且扩充部分是以b为直角边的直角三角形,则扩建后的等腰三角形花圃的周长为( )米.
A.32或20+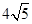 |
B.32或36或 |
C.32或 或20+ 或20+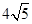 |
D.32或36或 或20+ 或20+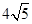 |
C
由于扩充所得的等腰三角形腰和底不确定,若设扩充所得的三角形是△ABD,则应分为①AB=AD,②AD=BD两种情况进行讨论.
解:如图所示:在Rt△ABC中,
∵AC=8m,BC=6m,
∴AB=10m,

如图1,当AB=AD时,CD=BC=6m,
此时等腰三角形花圃的周长=10+10+6+6=32(m);
如图2:当AD=BD时,设AD=BD=xm;
Rt△ACD中,BD=xm,CD=(x﹣6)m;
由勾股定理,得AD2=DC2+CA2,即(x﹣6)2+82=x2,解得x=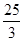 ;
;
此时等腰三角形绿地的周长=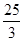 ×2+10=
×2+10= (m).
(m).
当AB=BD时,在Rt△ACD中,AD=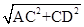 =
=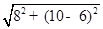 =
=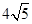 ,
,
∴等腰三角形绿地的周长=2×10+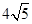 =20+
=20+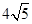 .
.
故选C.
解:如图所示:在Rt△ABC中,
∵AC=8m,BC=6m,
∴AB=10m,

如图1,当AB=AD时,CD=BC=6m,
此时等腰三角形花圃的周长=10+10+6+6=32(m);
如图2:当AD=BD时,设AD=BD=xm;
Rt△ACD中,BD=xm,CD=(x﹣6)m;
由勾股定理,得AD2=DC2+CA2,即(x﹣6)2+82=x2,解得x=
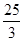 ;
;此时等腰三角形绿地的周长=
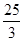 ×2+10=
×2+10= (m).
(m).当AB=BD时,在Rt△ACD中,AD=
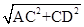 =
=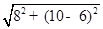 =
=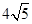 ,
,∴等腰三角形绿地的周长=2×10+
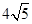 =20+
=20+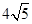 .
.故选C.

练习册系列答案
相关题目

 三者之间的关系,并用式子表示出来。
三者之间的关系,并用式子表示出来。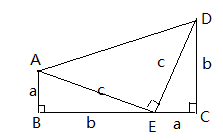
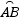 的中点,CD与AB的交点为E,则
的中点,CD与AB的交点为E,则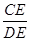 等于( )
等于( )