题目内容
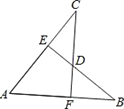
【题目】如图,AD是△ABC的角平分线,过点D向AB,AC两边作垂线,垂足分别为E,F,那么下列结论中不一定正确的是( )

A. BD=CD B. DE=DF C. AE=AF D. ∠ADE=∠ADF
【答案】A
【解析】
根据角平分线上的点到角的两边距离相等可得DE=DF,然后利用“HL”证明Rt△ADE和Rt△ADF全等,根据全等三角形对应边相等可得AE=AF,∠ADE=∠ADF.
解:如图,∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,
∴DE=DF,
在Rt△ADE和Rt△ADF中,
![]()
∴Rt△ADE≌Rt△ADF(HL),
∴AE=AF,∠ADE=∠ADF,即只有AB=AC时,BD=CD.
综上所述,结论错误的是BD=CD.
故选:A.

练习册系列答案
相关题目
【题目】一组对边平行,另一组对边相等且不平行的四边形叫做等腰梯形.
(1)类比研究
我们在学完平行四边形后,知道可以从对称性、边、角和对角线四个角度对四边形进行研究,完成表.
四边形 | 对称性 | 边 | 角 | 对角线 |
平行 | . | 两组对边分别平行,两组对边分别相等. | 两组对角 | 对角线互相平分. |
等腰 | 轴对称图形,过平行的一组对边中点的直线是它的对称轴. | 一组对边平行,另一组对边相等. | . | . |
(2)演绎论证
证明等腰梯形有关角和对角线的性质.
已知:在等腰梯形ABCD中,AD∥BC,AB=DC,AC、BD是对角线.
求证:
证明:
揭示关系
我们可以用图来揭示三角形和一些特殊三角形之间的关系.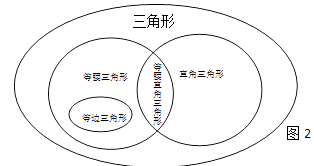
(3)请用类似的方法揭示四边形、对角线相等的四边形、平行四边形、矩形以及等腰梯形之间的关系.