题目内容
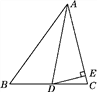
【题目】如图,在路边安装路灯,灯柱BC高15m,与灯杆AB的夹角ABC为120°.路灯采用锥形灯罩,照射范围DE长为18.9m,从D、E两处测得路灯A的仰角分别为∠ADE=80.5°,∠AED=45°.求灯杆AB的长度.(参考数据:cos80.5°≈0.2,tan80.5°≈6.0)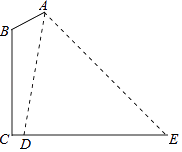
【答案】解:过点A作AF⊥CE,交CE于点F.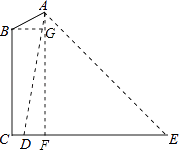
设AF的长度为xm.
∵∠AED=45°,
∴△AEF是等腰直角三角形.
∴EF=AF=x.
在Rt△ADF中,∵tan∠ADF= ![]() ,
,
∴DF= ![]() =
= ![]() =
= ![]() .
.
∵DE=18.9,
∴ ![]() +x=18.9,
+x=18.9,
解得x=16.2,
过点B作BG⊥AF,交AF于点G,
则BC=GF=15,∠CBG=90°.
∴AG=AF﹣GF=16.2﹣15=1.2,
∵∠ABC=120°,
∴∠ABG=∠ABC﹣∠CBG=120°﹣90°=30°.
在Rt△ABG中,
∵sin∠ABG= ![]() ,
,
∴AB= ![]() =
= ![]() =2.4,
=2.4,
答:灯杆AB的长度为2.4 m.
【解析】过点A作AF⊥CE,点B作BG⊥AF,根据正切的概念求出DF,列方程求出AF,根据正弦的概念计算即可.
【考点精析】解答此题的关键在于理解特殊角的三角函数值的相关知识,掌握分母口诀:30度、45度、60度的正弦值、余弦值的分母都是2,30度、45度、60度的正切值、余切值的分母都是3,分子口诀:“123,321,三九二十七”.

 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案【题目】新房装修后,甲居民购买家居用品的清单如下表,因污水导致部分信息无法识别,根据下表解决问题:
家居用品名称 | 单价(元) | 数量(个) | 金额(元) |
挂钟 | 30 | 2 | 60 |
垃圾桶 | 15 | ||
塑料鞋架 | 40 | ||
艺术饰品 | a | 2 | 90 |
电热水壶 | 35 | 1 | b |
合计 | 8 | 280 | |
(1)直接写出a= ,b= ;
(2)甲居民购买了垃圾桶,塑料鞋架各几个?
(3)若甲居民再次购买艺术饰品和垃圾桶两种家居用品,共花费150元,则有哪几种不同的购买方案?