题目内容
【题目】(1)计算:(a+b)2﹣b(2a+b)
(2)解不等式:(3x+4)(3x-4)<9(x-2)(x+3)
【答案】(1)a2;(2)x>![]() .
.
【解析】
(1)根据完全平方公式,以及单项式与多项式相乘,先用单项式乘多项式的每一项,再把所得的积相加计算即可;
(2)首先利用多项式的乘法法则化简等号两边的式子,然后移项、合并同类项、系数化为1即可求得不等式的解集.
(1)(a+b)2-b(2a+b)=a2+2ab+b2-2ab-b2=a2;
(2)(3x+4)(3x-4)<9(x-2)(x+3),
9x2-16<9(x2+x-6),
即9x2-16<9x2+9x-54,
移项,得9x2-9x2-9x<-54+16,
合并同类项,得-9x<-38,
系数化为1得x>![]() .
.

练习册系列答案
相关题目
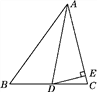
【题目】如图,AD是△ABC的角平分线,过点D向AB,AC两边作垂线,垂足分别为E,F,那么下列结论中不一定正确的是( )

A. BD=CD B. DE=DF C. AE=AF D. ∠ADE=∠ADF
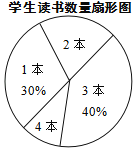
【题目】某校七年级共有500名学生,在“世界读书日”前夕,开展了“阅读助我成长”的读书活动.为了解该年级学生在此次活动中课外阅读情况,童威随机抽取m名学生,调查他们课外阅读书籍的数量,将收集的数据整理成如下统计表和扇形图.
学生读书数量统计表
阅读量/本 | 学生人数 |
1 | 15 |
2 | a |
3 | b |
4 | 5 |
(1)直接写出m、a、b的值;
(2)估计该年级全体学生在这次活动中课外阅读书籍的总量大约是多少本?