Question

【题目】完成下面的证明

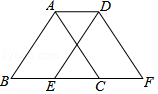
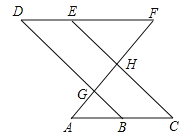
如图，点E在直线DF上，点B在直线AC上，若∠AGB=∠EHF，∠C=∠D.

求证：∠A=∠F.

证明：∵∠AGB=∠EHF

∠AGB=___________（对顶角相等）

∴∠EHF=∠DGF

∴DB∥EC（____________________________________）

∴∠_________=∠DBA（________________________________）

又∵∠C=∠D

∴∠DBA=∠D

∴DF∥_______（__________________________________）

∴∠A=∠F（__________________________________）.

Answer 1

【答案】 ∠DGF 同位角相等，两直线平行 C 两直线平行，同位角相等 AC 内错角相等，两直线平行 两直线平行，内错角相等

【解析】试题分析：根据对顶角相等推知同位角∠EHF=∠DGF，从而证得两直线DB∥EC；然后由平行线的性质知内错角∠DBA=∠D，即可根据平行线的判定定理推知两直线DF∥AC；最后由平行线的性质（两直线平行，内错角相等）证得∠A=∠F．

试题解析：解：∵∠AGB=∠EHF，∠AGB=∠DGF（对顶角相等），∴∠EHF=∠DGF

，∴DB∥EC（同位角相等，两直线平行），∴∠C=∠DBA （ 两直线平行，同位角相等）；

又∵∠C=∠D（已知），∴∠DBA=∠D（等量代换），∴DF∥AC（内错角相等，两直线平行），∴∠A=∠F（两直线平行，内错角相等）．