��Ŀ����
����Ŀ���з��̽�Ӧ���⣺�����������ع������ĵ�һ����5000Ԫ�����ס���������Ʒ����������Ʒ�ļ����ȼ���Ʒ������![]() ����15�����ס���������Ʒ�Ľ��ۺ��ۼ����±���ע������=�ۼ۩����ۣ�
����15�����ס���������Ʒ�Ľ��ۺ��ۼ����±���ע������=�ۼ۩����ۣ�
�� | �� | |
���ۣ�Ԫ/���� | 20 | 30 |
�ۼۣ�Ԫ/���� | 29 | 40 |
��1�������ع������Ľ���һ�ι����ļס���������Ʒȫ�������һ���ɻ�ö�������
��2���ù������ĵڶ����Ե�һ�εĽ����ֹ����ס���������Ʒ�����м�����Ʒ�ļ������䣬������Ʒ�ļ����ǵ�һ�ε�3��������Ʒ��ԭ�����ۣ�����Ʒ�������ۣ��ڶ���������Ʒ���������Ժ���������ȵ�һ�λ�õ��������160Ԫ����ڶ���������Ʒ�ǰ�ԭ�۴������ۣ�
���𰸡���1��������Ʒȫ�������ɻ��1970Ԫ������2���ڶ���������Ʒ�ǰ�ԭ�۴�8.5�����ۣ�
��������
�����������1�����һ�ι���������Ʒx������������Ʒ�ļ����ǣ�![]() x+15����������ϵ�ǣ�����x��������Ʒ�Ľ���+������
x+15����������ϵ�ǣ�����x��������Ʒ�Ľ���+������![]() x+15����������Ʒ�Ľ���=5000�������г����������⼴�ɣ�
x+15����������Ʒ�Ľ���=5000�������г����������⼴�ɣ�
��2����ڶ���������Ʒ�ǰ�ԭ�۴�y�����ۣ����ݵڶ���������Ʒ���������Ժ���������ȵ�һ�λ�õ��������160Ԫ�������̣������⼴�ɣ�
�⣺��1�����һ�ι���������Ʒx�������ҵļ���Ϊ��![]() x+15��������������ã�
x+15��������������ã�
20x+30��![]() x+15��=5000��
x+15��=5000��
��� x=130��
��![]() x+15=65+15=80��������
x+15=65+15=80��������
��29��20����130+��40��30����80=1970��Ԫ����
��������Ʒȫ�������ɻ��1970Ԫ����
��2����ڶ���������Ʒ�ǰ�ԭ�۴�y�����ۣ�
�����⣬�У�29��20����130+��40��![]() ��30����80��3=1970+160��
��30����80��3=1970+160��
��� y=8.5��
�𣺵ڶ���������Ʒ�ǰ�ԭ�۴�8.5�����ۣ�

����Ŀ��2013��5��23�������н������˴���Ʒ��������д��������꼶��ѧ�о�ѧϰС����ijʮ��·��������鲿������Ը÷�����˽������ͳ�ƽ�����������ͼ��������������ͳ��ͼ������ͼ��������ݻش��������⣮
�÷� | |
A | 50��n��60 |
B | 60��n��70 |
C | 70��n��80 |
D | 80��n��90 |
E | 90��n��100 |
��1����������������
��2����ȫƵ���ֲ�ͼ�� 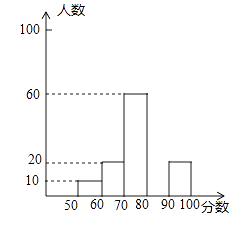
��3��������ͳ��ͼ�У���B�����ڵ����ε�Բ�ĽǵĶ���Ϊ�� 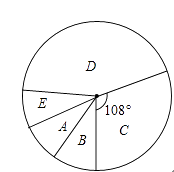
��4��������һ�����·�ڹ���2000��ͨ������ɹ��Ƶ÷���80���ϵ�������ԼΪ ��