Question

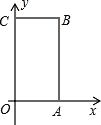
【题目】如图1，已知射线CB∥OA，∠C=∠OAB，

（1）求证：AB∥OC；

（2）如图2，E、F在CB上，且满足∠FOB=∠AOB，OE平分∠COF.

①当∠C=110°时，求∠EOB的度数.

②若平行移动AB，那么∠OBC :∠OFC的值是否随之发生变化？若变化，找出变

化规律；若不变，求出这个比值.

Answer 1

【答案】（1）见解析；（2）①35°，②∠OBC:∠OFC的值不发生变化，∠OBC:∠OFC=1:2

【解析】试题分析：（1）由平行线的性质得到∠C+∠COA=180°，再由∠C=∠OAB，得到∠OAB+∠COA=180°，根据同旁内角互补，两直线平行即可得到结论；

（2）①先求出∠COA的度数，由∠FOB=∠AOB，OE平分∠COF， 即可得到结论；

②∠OBC：∠OFC的值不发生变化．由平行线的性质可得∠OBC=∠BOA，∠OFC=∠FOA．

由FOB=∠AOB，得到∠OFC=2∠OBC，从而得出结论．

试题解析：解：（1）∵CB∥OA， ∴∠C+∠COA=180°．

∵∠C=∠OAB，∴∠OAB+∠COA=180°，∴AB∥OC；

（2）①∠COA=180°-∠C=70°．∵∠FOB=∠AOB，OE平分∠COF， ∴ ∠FOB+∠EOF= （∠AOF+∠COF）= ∠COA=35°；

②∠OBC：∠OFC的值不发生变化．

∵CB∥OA，∴∠OBC=∠BOA，∠OFC=∠FOA．

∵∠FOB=∠AOB，∴∠FOA=2∠BOA，∴∠OFC=2∠OBC，∴∠OBC：∠OFC=1：2．