题目内容
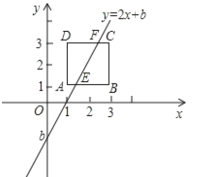
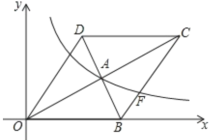
【题目】如图,在平面直角坐标系中,平行四边形OBCD的边OB在x轴正半轴上,反比例函数y=![]() (x>0)的图象经过该平行四边形对角线的交点A,且与边BC交于点F.若点D的坐标为(6,8)且OD=DC,则点F的坐标是________.
(x>0)的图象经过该平行四边形对角线的交点A,且与边BC交于点F.若点D的坐标为(6,8)且OD=DC,则点F的坐标是________.
【答案】(12, ![]() )
)
【解析】
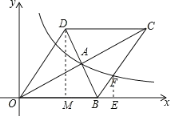
过点D作DM⊥x轴于点M,过点F作FE⊥x于点E,先用勾股定理求出OD,再根据条件判定四边形OBCD是菱形,求出对角线交点A的坐标,即可得到反比例函数解析式,再求出直线BC解析式,设出F点坐标,根据F点在反比例函数图像上,可建立方程求解.
如图,过点D作DM⊥x轴于点M,过点F作FE⊥x于点E,
∵点D的坐标为(6,8),
∴OD=![]() ,
,
∵平行四边形OBCD中OD=DC,
∴四边形OBCD是菱形,
∴OB=OD=10,
∴点B的坐标为(10,0),
∵点A为菱形OBCD对角线的交点,
∴点A是BD的中点,坐标为(8,4),
∵点A在反比例函数y=![]() 上,
上,
∴k=xy=8×4=32,
∴反比例函数解析式为y=![]()
∵OD∥BC,OD直线的斜率![]()
∴设BC直线解析式为![]() ,将B (10,0)代入解析式得
,将B (10,0)代入解析式得
![]() ,解得
,解得![]() ,
,
∴BC直线解析式为![]()
点F在BC上,设F点坐标为(![]() )
)
∵点F在反比例函数![]() 上,
上,
∴![]() ,
,
即![]() ,
,
解得:![]() ,
,![]() (舍去),
(舍去),
当![]() 时,
时,![]()
∴点F的坐标为:(12, ![]() ).
).
故答案为:(12, ![]() )
)

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目