题目内容
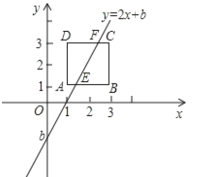
【题目】如图,已知正方形ABCD的顶点A(1,1),B(3,1),直线y=2x+b交边AB于点E,交边CD于点F,则直线y=2x+b 在y 轴上的截距b的变化范围是__________.
【答案】3≤b≤1
【解析】
由于直线y=2x+b交AB于点E,交CD于点F,所以点E在线段AB上,最左端是A点,于是把A的坐标代入可求得一个b值,同理,F的最右端为点C,代入C的左标可求出b的另一个值,答案可得.
∵四边形ABCD是正方形,A(1,1),B(3,1)
∴C点坐标为(3,3)
∵直线y=2x+b交边AB于点E,交边CD于点F
∴所以点E在线段AB上,最左端是A点,
当直线通过点A时,将A(1,1)代入y=2x+b得,
![]() ,解得
,解得![]() ;
;
F点在CD上,最右端为C,
当直线通过点C时,将C(3,3)代入y=2x+b得,
![]() ,解得
,解得![]() ,
,
∴b的范围为3≤b≤1.
故答案为:3≤b≤1.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目