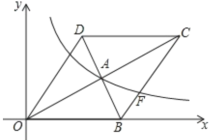
题目内容
【题目】如图,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为对角线
为对角线![]() 上异于点
上异于点![]() 的一个动点,联结
的一个动点,联结![]() ,将
,将![]() 沿
沿![]() 所在的直线翻折,使得点
所在的直线翻折,使得点![]() 落在点
落在点![]() 的位置
的位置
(1)当![]() 时,求点
时,求点![]() 到直线
到直线![]() 的距离。
的距离。
(2)联结![]() 交
交![]() 于
于![]() ,求当
,求当![]() 和
和![]() 相似时,线段
相似时,线段![]() 的长。
的长。
(3)当![]() 时,请直接写出此时
时,请直接写出此时![]() 的面积。
的面积。
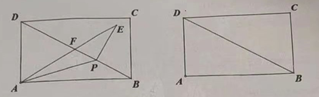
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)根据直角三角形性质求解即可
(2)根据题意,相似分为两种情况 ,一是△EPF∽△BAD,二是△EFP∽△BAD,在两种情况下分类讨论,分别求出不同情况下的值
(3)如图一、图二,首先弄清楚题目所存在的情况可能性,之后按照特殊的四边形性质以及三角形相关性质求解即可
解 (1)过E作EG⊥AB于点G,
在Rt△ABD中,AD=![]() , AB=3,
, AB=3,
∴∠ABD =30°,
∵∠APD=45°,
∴∠BAP=15°,
∴∠BAE = 30°
在Rt△EAG中,EA= EB=3
∴EG=![]()
(2)①△EPF∽△BAD,
∴∠EPF = 90° ,
∵∠APB=∠APE,
∴180°-∠APD=90 °+∠APD,
∴∠APD=45°,在△APD中,∠ADP=60°,∠APD=45°,AD=![]() ,DP=
,DP=![]()
∵ BD=![]()
∴BP=![]()
②△EFP∽△BAD,
∴AE⊥BD,
∴∠BAF=60°,
∴∠PAD=30°,
∴AP= BP
在等腰△APB中,AB=3, ∠APB=30°,
∴BP=![]()
综上所述:当△EPF和△ABD相似时,BP=![]() 或
或![]()
(3)

如图一:∠DPE=30°,
∵∠APB=∠APE,
∴180°-∠APD=30°+∠APD,
∴∠APD=75°
∴∠PAB=45°
在△APB中,过P做PI⊥AB
AB=3,∠PAB=45°,∠PBA=30°
∴PI=![]()
∴△APB面积=![]()
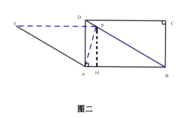
如图二:过P做PH⊥AB于H,易得四边形PEAB为菱形
∴△APB面积=![]()
综上所述,△APB面积为![]() 或
或![]()

【题目】某位篮球运动员在同样的条件下进行投篮练习,结果如下表:
投篮次数 |
|
|
|
|
|
|
|
进球次数 |
|
|
|
|
|
|
|
进球频率 | ________ | ________ | ________ | ________ | ________ | ________ | ________ |
![]() 将上表补充完整;
将上表补充完整;
![]() 这位运动员投篮一次,进球的概率约是多少?
这位运动员投篮一次,进球的概率约是多少?
![]() 若这位运动员投篮
若这位运动员投篮![]() 次,必定会投进
次,必定会投进![]() 次吗?为什么?
次吗?为什么?