题目内容
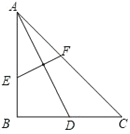
【题目】如图,已知在△ABC中,∠B=90°,AB=BC,AD是BC边上的中线,EF是AD的垂直平分线,交AB于点E,交AC于点F,则AE:BE的值为_______.
【答案】![]()
【解析】
连接DE,设BD=k,BE=x,则DC=k,AB=2k,AE=2k-x,由中垂线的性质可得AE=DE,然后在Rt△BDE中,利用勾股定理建立方程可求出BE,再求AE,即可得到比值.
如图,连结DE.

设BD=k,BE=x,则DC=k,AB=2k,AE=2k-x.
∵EF是AD的垂直平分线,
∴AE=DE=2k-x,
∵∠B=90°,
∴在Rt△BDE中,DE2=BD2+BE2=k2+x2,
∴(2k-x)2=k2+x2,
∵k≠0,
∴x=![]() ,
,
∴BE=![]() ,AE=2k-
,AE=2k-![]() =
=![]() ,
,
∴AE:BE=![]() :
:![]() =
=![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目
【题目】某位篮球运动员在同样的条件下进行投篮练习,结果如下表:
投篮次数 |
|
|
|
|
|
|
|
进球次数 |
|
|
|
|
|
|
|
进球频率 | ________ | ________ | ________ | ________ | ________ | ________ | ________ |
![]() 将上表补充完整;
将上表补充完整;
![]() 这位运动员投篮一次,进球的概率约是多少?
这位运动员投篮一次,进球的概率约是多少?
![]() 若这位运动员投篮
若这位运动员投篮![]() 次,必定会投进
次,必定会投进![]() 次吗?为什么?
次吗?为什么?