题目内容
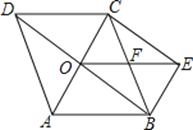
【题目】如图，在
中，
，
，
分别是
，
上的动点，将
沿
折叠.
(1)当点
与点
重合时，如图1.若
，
，则
的周长为_____.
(2)定义：若在三角形中，期中一条边是另一条边的2倍，则称这个三角形为“倍边三角形”.当点与点
重合时，如图2.若
，则
是倍边三角形吗？请说明理由.
【答案】(1)16；(2)△ACE是倍边三角形，理由见解析.
【解析】
（1）将△ACD的周长转化为求AC与AB的和即可.
（2）只需求出2CE=AE即可.
（1）∵BD=CD，
∴△ACD的周长=AC+AD+CD=AC+AD+BD=AC+AB=10+6=16，
（2）∵AB=2AC，
∴∠B=30°，
∵AE=EB，∠ACB=90°，
∴∠CAE=∠EAB=∠B=30°，
∴2CE=AE，
∴△ACE是倍边三角形.
【题目】为降低空气污染，公交公司决定全部更换节能环保的燃气公交车．计划购买A型和B型两种公交车共10辆，其中每台的价格，年均载客量如表：
A型 | B型 | |
价格（万元/辆） | a | b |
年均载客量（万人/年/辆） | 60 | 100 |
若购买A型公交车1辆，B型公交车2辆，共需400万元；若购买A型公交车2辆，B型公交车1辆，共需350万元
（1）求购买每辆A型公交车和每辆B型公交车分别多少万元？
（2）如果该公司购买A型和B型公交车的总费用不超过1200万元，且确保这10辆公交车年均载客总和不少于680万人次，有哪几种购车方案？请你设计一个方案，使得购车总费用最少．
【题目】“金山”超市现有甲、乙两种糖果若干kg，两种糖果的售价和进价如表
糖果 | 甲种 | 乙种 |
售价 | 36元/kg | 20元/kg |
进价 | 30元/kg | 16元/kg |
（1）超市准备用甲、乙两种糖果混合成杂拌糖出售，混合后糖果的售价是27.2元/kg，现要配制这种杂拌糖果100/kg，需要甲、乙两种糖果各多少千克？
（2）“六一”儿童节前夕，超市准备用5000元购进甲、乙两种糖果共200kg，如何进货才能使这批糖果获得最大利润，最大利润是多少？（注：进货量只能为整数）
