题目内容
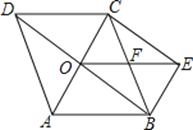
【题目】如图所示,点O是菱形ABCD对角线的交点,CE∥BD,EB∥AC,连接OE,交BC于F.
(1)求证:OE=CB;
(2)如果OC: OB=1:2,OE=![]() ,求菱形ABCD的面积.
,求菱形ABCD的面积.
【答案】(1)证明见解析;
(2)S菱形ABCD=4
【解析】
试题(1)通过证明四边形OCEB是矩形来推知OE=CB;
(2)利用(1)中的AC⊥BD、OE=CB,结合已知条件,在Rt△BOC中,由勾股定理求得CO=1,OB=2.然后由菱形的对角线互相平分和菱形的面积公式进行解答.
试题解析:(1)∵四边形ABCD是菱形
∴AC⊥BD
∵CE//DB,BE//AC
∴四边形OCEB是平行四边形
∴四边形OCEB是矩形
∴OE=BC
∵四边形OCEB是矩形
∴BC=OE=![]()
∵AC⊥BD
∴Rt△BCO中,CO2+OB2=BC2=![]() =5
=5
又CO:OB=1:2
∴CO=1,OB=2
∵四边形ABCD是菱形
∴AC=2,BD=4
∴S菱形ABCD=![]() BD×AC=4
BD×AC=4

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目