Question

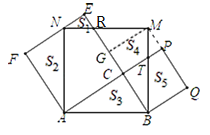
【题目】如图，以AB为斜边的Rt△ABC的每条边为边作三个正方形，分别是正方形ABMN，正方形BCPQ，正方形ACEF，且边EF恰好经过点N．若S3＝S4＝6，则S1+S5＝_____．（注：图中所示面积S表示相应封闭区域的面积，如S3表示△ABC的面积）

Answer 1

【答案】6

【解析】

如图，连接MQ，作MG⊥EC于G，设PC交BM于T,MN交EC于R．先证明△ABC≌△MBQ（SAS），推出∠ACB＝∠BQM＝90°，由∠PQB＝90°，推出M，P，Q共线，由四边形CGMP是矩形，推出MG＝PC＝BC，证明△MGR≌△BCT（AAS），推出MR＝BT，由MN＝BM，NR＝MT，可证△NRE≌MTP，推出S1+S5＝S3＝6.

如图，连接MQ，作MG⊥EC于G，设PC交BM于TMN交EC于R．

∵∠ABM＝∠CBQ＝90°，

∴∠ABC＝∠MBQ，

∵BA＝BM，BC＝BQ，

在△ABC和△MBQ，

，

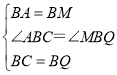∴△ABC≌△MBQ（SAS），

∴∠ACB＝∠BQM＝90°，

∵∠PQB＝90°，

∴M，P，Q共线，

∵四边形CGMP是矩形，

∴MG＝PC＝BC，

∵∠BCT＝∠MGR＝90°，∠BTC+∠CBT＝90°，∠BRM+∠CBT＝90°，

∴∠MRG＝∠BTC，

在△MGR和△BCT中

，

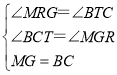∴△MGR≌△BCT（AAS），

∴MR＝BT，

又∵MN＝BM，

∴NR＝MT，，

在△NRE和MTP，

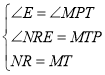
∴△NRE≌MTP（AAS），

∴S1+S5＝S3＝6，

故答案是：6．