Question

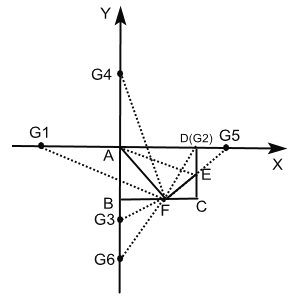
【题目】如图，在矩形ABCD中，已知AB=8cm，BC=10cm，折叠矩形的一边AD，使点D落在BC边上的点F处，折痕为AE．以点A为原点，分别以AD所在的直线为x轴，AB所在的直线为y轴建立坐标系.

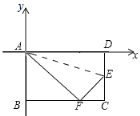
（1）写出点B、D、E、F的坐标；

（2）在坐标轴上是否存在点G，使△AFG是以AF为腰长的等腰三角形？若存在，请求出点G的坐标；若不存在，请说明理由.

Answer 1

【答案】（1）B（0，－8），D（10，0），E（10，－5），F（6，－8）；（2）点G的坐标为：（－10，0）或（10，0）或（0，－10）或（0，10）或（12，0）或（0，－16）.

【解析】

（1）由题意可得B，D坐标，AD=AF=10cm，然后利用勾股定理求出BF可得F点坐标，设EF=DE=x，在Rt△EFC中，利用勾股定理构造方程求出EF=DE=5cm，可得E点坐标；

（2）分情况讨论：①当AF=AG时，②当AF=FG时，分别利用AF=AG=10cm和点F坐标求出所有符合题意的点G坐标即可.

解：（1）∵AB=8cm，BC=10cm，

∴CD=8cm，AD=10cm，

∴B（0，－8），D（10，0），

根据折叠的性质可得：AD=AF=10cm，

∴BF=cm，

∴F（6，－8），

设EF=DE=x，则EC=8-x，FC=BC-BF=4cm，

∴在Rt△EFC中，EF2=EC2+FC2，即x2=（8-x）2+42，

解得：x=5，

∴EF=DE=5cm，

∴E（10，－5），

综上所述：B（0，－8），D（10，0），E（10，－5），F（6，－8）；

（2）∵AF=10cm，△AFG是以AF为腰长的等腰三角形且点G在坐标轴上，

∴①当AF=AG=10cm时，

如图所示：G1（－10，0），G2（10，0），G3（0，－10），G4（0，10）；

②当AF=FG时，

∵F（6，－8），

∴G5（12，0），G6（0，－16），

综上所述：点G的坐标为：（－10，0）或（10，0）或（0，－10）或（0，10）或（12，0）或（0，－16）.