Question

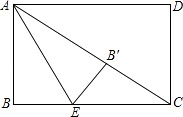
【题目】如图，已知长方形ABCD中，AD＝6cm，AB＝4cm，点E为AD的中点．若点P在线段AB上以1cm/s的速度由点A向点B运动，同时，点Q在线段BC上由点B向点C运动．

(1)若点Q的运动速度与点P的运动速度相等，经过1秒后，△AEP与△BPQ是否全等，请说明理由，并直接写出此时线段PE和线段PQ的位置关系；

(2)若点Q的运动速度与点P的运动速度相等，运动时间为t秒，设△PEQ的面积为Scm2，请用t的代数式表示S；

(3)若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△AEP与△BPQ全等？

Answer 1

【答案】（1）全等。理由见解析；（2）S=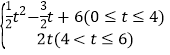；（3）点Q运动的速度为=3÷2=1.5cm/秒时，△AEP≌△BQP..

【解析】

（1）本题很容易证明△AEP≌△BPQ，这样可得出∠AEP=∠BPQ，因为∠AEP+∠APE=90°，可得出∠BPQ+∠APE=90°，这即可判断出结论．
（2）可分别用t表示出AP、BQ、BP的长度，然后用梯形的面积减去△APE、△BPQ的面积即可得出△PEQ的面积为Scm2．
（3）设Q运动的速度为xcm/s，则根据△AEP与△BQP得出AP=BP、AE=BQ，解出即可得出答案．

（1）全等,

理由：当t=1时，AP=1，BQ=1，∴AP=BQ．

∵E是AD的中点，∴

∵PB=AB=AP=4﹣1=3，∴AE=PB．

在Rt△EAP和Rt△PBQ中，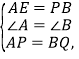

∴△EAP≌Rt△PBQ（SAS）．

此时.

（2）如图1所示连接QE．

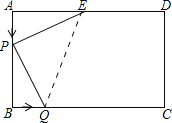
图1

当t≤4时，AP=BQ=t，

S梯形AEQB

∴

如图2所示：

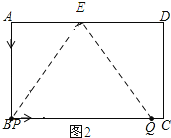
当4＜t≤6时，点P与点B重合，

∴S与t的函数关系式为S=；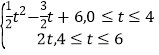

（t的取值范围不做要求）

（3）如图3所示：

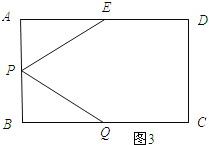
∵△AEP≌△BQP，PA≠BQ，

∴AP=PB=2，AE=BQ=3．

∴

∴点Q运动的速度为=3÷2=1.5cm/秒时，△AEP≌△BQP..