题目内容
【题目】在平面直角坐标系中,点![]() ,
,![]() ,点C为x轴正半轴上一动点,过点A作
,点C为x轴正半轴上一动点,过点A作![]() 交y轴于点E.
交y轴于点E.
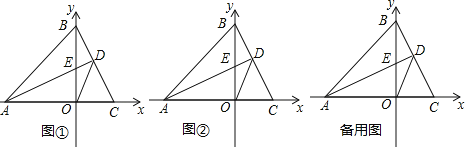
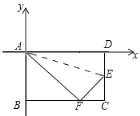
![]() 如图
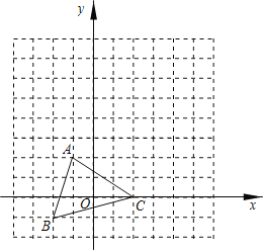
如图![]() ,若点C的坐标为
,若点C的坐标为![]() ,试求点E的坐标;
,试求点E的坐标;
![]() 如图
如图![]() ,若点C在x轴正半轴上运动,且
,若点C在x轴正半轴上运动,且![]() , 其它条件不变,连接DO,求证:OD平分
, 其它条件不变,连接DO,求证:OD平分![]()
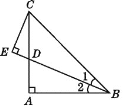
![]() 若点C在x轴正半轴上运动,当
若点C在x轴正半轴上运动,当![]() 时,求
时,求![]() 的度数.
的度数.
【答案】(1)点E的坐标为(0,2);(2)详见解析;(3)∠OCB=60°.
【解析】
(1)先根据AAS判定△AOE≌△BOC,得出OE=OC,再根据点C的坐标为(2,0),得到OC=2=OE,进而得到点E的坐标;
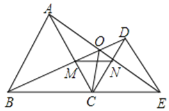
(2)先过点O作OM⊥AD于点M,作ON⊥BC于点N,根据△AOE≌△BOC,得到S△AOE=S△BOC,且AE=BC,再根据OM⊥AE,ON⊥BC,得出OM=ON,进而得到OD平分∠ADC;
(3)在DA上截取DP=DC,连接OP,根据SAS判定△OPD≌△OCD,再根据三角形外角性质以及三角形内角和定理,求得∠PAO=30°,进而得到∠OCB=60°.
(1)如图①,∵AD⊥BC,BO⊥AO,
∴∠AOE=∠BDE,
又∵∠AEO=∠BED,
∴∠OAE=∠OBC,
∵A(-3,0),B(0,3),
∴OA=OB=3,
∴△AOE≌△BOC,
∴OE=OC,
又∵点C的坐标为(2,0),
∴OC=2=OE,
∴点E的坐标为(0,2);
(2)如图②,过点O作OM⊥AD于点M,作ON⊥BC于点N,

∵△AOE≌△BOC,
∴S△AOE=S△BOC,且AE=BC,
∵OM⊥AE,ON⊥BC,
∴OM=ON,
∴OD平分∠ADC;
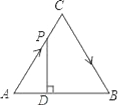
(3)如所示,在DA上截取DP=DC,连接OP,

∵∠PDO=∠CDO,OD=OD,
∴△OPD≌△OCD,
∴OC=OP,∠OPD=∠OCD,
∵AD-CD=OC,
∴AD-DP=OP,即AP=OP,
∴∠PAO=∠POA,
∴∠OPD=∠PAO+∠POA=2∠PAO=∠OCB,
又∵∠PAO+∠OCD=90°,
∴3∠PAO=90°,
∴∠PAO=30°,
∴∠OCB=60°.

 小学同步三练核心密卷系列答案
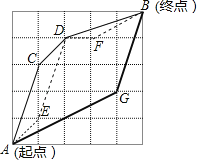
小学同步三练核心密卷系列答案【题目】嘉嘉参加机器人设计活动,需操控机器人在5×5的方格棋盘上从A点行走至B点,且每个小方格皆为正方形,主办单位规定了三条行走路径R1,R2,R3,其行经位置如图与表所示:
路径 | 编号 | 图例 | 行径位置 |
第一条路径 | R1 | _ | A→C→D→B |
第二条路径 | R2 | … | A→E→D→F→B |
第三条路径 | R3 | ▂ | A→G→B |
已知A、B、C、D、E、F、G七点皆落在格线的交点上,且两点之间的路径皆为直线,在无法使用任何工具测量的条件下,请判断R1、R2、R3这三条路径中,最长与最短的路径分别为何?请写出你的答案,并完整说明理由.