题目内容
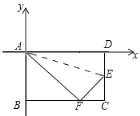
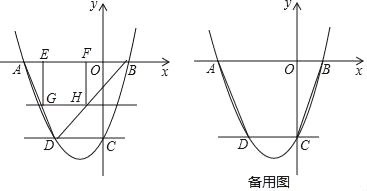
【题目】如图,已知抛物线y=ax2+bx﹣3与x轴交于点A(﹣3,0)和点B(1,0),交y轴于点C,过点C作CD∥x轴,交抛物线于点D.
(1)求抛物线的解析式;
(2)若直线y=m(﹣3<m<0)与线段AD、BD分别交于G、H两点,过G点作EG⊥x轴于点E,过点H作HF⊥x轴于点F,求矩形GEFH的最大面积;
(3)若直线y=kx+1将四边形ABCD分成左、右两个部分,面积分别为S1,S2,且S1:S2=4:5,求k的值.
【答案】(1)y=x2+2x﹣3;(2)3;(3)![]()
【解析】(1)利用待定系数法即可得出结论;
(2)先利用待定系数法求出直线AD,BD的解析式,进而求出G,H的坐标,进而求出GH,即可得出结论;
(3)先求出四边形ADNM的面积,再求出直线y=kx+1与线段CD,AB的交点坐标,即可得出结论.
(1)∵抛物线y=ax2+bx-3与x轴交于点A(-3,0)和点B(1,0),
∴![]() ,
,
∴![]() ,
,
∴抛物线的解析式为y=x2+2x-3;
(2)由(1)知,抛物线的解析式为y=x2+2x-3,
∴C(0,-3),
∴x2+2x-3=-3,
∴x=0或x=-2,
∴D(-2,-3),
∵A(-3,0)和点B(1,0),
∴直线AD的解析式为y=-3x-9,直线BD的解析式为y=x-1,
∵直线y=m(-3<m<0)与线段AD、BD分别交于G、H两点,
∴G(-![]() m-3,m),H(m+1,m),
m-3,m),H(m+1,m),
∴GH=m+1-(-![]() m-3)=
m-3)=![]() m+4,
m+4,
∴S矩形GEFH=-m(![]() m+4)=-
m+4)=-![]() (m2+3m)=-
(m2+3m)=-![]() (m+
(m+![]() )2+3,
)2+3,
∴m=-![]() ,矩形GEFH的最大面积为3.
,矩形GEFH的最大面积为3.
(3)∵A(-3,0),B(1,0),
∴AB=4,
∵C(0,-3),D(-2,-3),
∴CD=2,
∴S四边形ABCD=![]() ×3(4+2)=9,
×3(4+2)=9,
∵S1:S2=4:5,
∴S1=4,
如图,

设直线y=kx+1与线段AB相交于M,与线段CD相交于N,
∴M(-![]() ,0),N(-
,0),N(-![]() ,-3),
,-3),
∴AM=-![]() +3,DN=-
+3,DN=-![]() +2,
+2,
∴S1=![]() (-
(-![]() +3-
+3-![]() +2)×3=4,
+2)×3=4,
∴k=![]()