Question

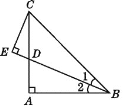
【题目】如图，以Rt△ABC的直角边AB为直径作⊙O交斜边AC于点D，过圆心O作OE∥AC，交BC于点E，连接DE．

（1）判断DE与⊙O的位置关系并说明理由；

（2）求证：2DE2=CDOE；

（3）若tanC=，DE=，求AD的长．

Answer 1

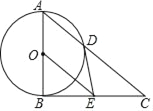
【答案】（1）DE是⊙O的切线，理由见解析；（2）证明见解析；（3）

【解析】（1）先判断出DE=BE=CE，得出∠DBE=∠BDE，进而判断出∠ODE=90°，即可得出结论；

（2）先判断出△BCD∽△ACB，得出BC2=CDAC，再判断出DE=BC，AC=2OE，即可得出结论；

（3）先求出BC，进而求出BD，CD，再借助（2）的结论求出AC，即可得出结论．

（1）DE是⊙O的切线，理由：如图，

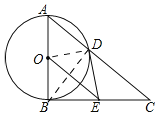
连接OD，BD，∵AB是⊙O的直径，

∴∠ADB=∠BDC=90°，

∵OE∥AC，OA=OB，

∴BE=CE，

∴DE=BE=CE，

∴∠DBE=∠BDE，

∵OB=OD，

∴∠OBD=∠ODB，

∴∠ODE=∠OBE=90°，

∵点D在⊙O上，

∴DE是⊙O的切线；

（2）∵∠BCD=∠ABC=90°，∠C=∠C，

∴△BCD∽△ACB，

∴，

∴BC2=CDAC，

由（1）知DE=BE=CE=BC，

∴4DE2=CDAC，

由（1）知，OE是△ABC是中位线，

∴AC=2OE，

∴4DE2=CD2OE，

∴2DE2=CDOE；

（3）∵DE=，

∴BC=5，

在Rt△BCD中，tanC=，

设CD=3x，BD=4x，根据勾股定理得，（3x）2+（4x）2=25，

∴x=-1（舍）或x=1，

∴BD=4，CD=3，

由（2）知，BC2=CDAC，

∴AC=，

∴AD=AC-CD=-3=．