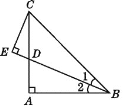
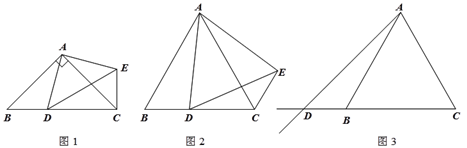
[题目](1)如图①.已知△ABC为直角三角形.∠A＝90°.若沿图中虚线剪去∠A.则∠1+∠2等于( )A．90° B．135° C．270° D．315°(2)如图②.已知△ABC中.∠A＝40°.剪去∠A后成四边形.则∠1+∠2＝ °,(3)根据(1)与(2)的求解过程.请你归纳猜想∠1+∠2与∠A的关系是．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】(1)如图①，已知△ABC为直角三角形，∠A＝90°，若沿图中虚线剪去∠A，则∠1＋∠2等于(　　)

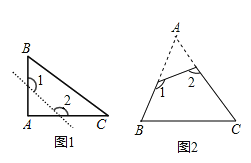
A．90° B．135° C．270° D．315°

(2)如图②，已知△ABC中，∠A＝40°，剪去∠A后成四边形，则∠1＋∠2＝________°；

(3)根据(1)与(2)的求解过程，请你归纳猜想∠1＋∠2与∠A的关系是______________．

【答案】（1）C；（2）220；（3）∠1＋∠2＝180°＋∠A.

【解析】

（1）利用了四边形内角和为360°和直角三角形的性质求解；
（2）根据三角形的外角等于与它不相邻的两个内角和求解；
（3）根据（1）（2）可以直接写出结果；

解：(1)∵四边形的内角和为360°，直角三角形中两个锐角的和为90°，

∴∠1＋∠2＝360°－(∠C＋∠B)＝360°－90°＝270°.

故选C.

(2)在△ABC中，∠A＝40°，

∠C＋∠B＝180°－40°=140°

∴∠1＋∠2＝360°－(∠C＋∠B)＝220°，

故答案是：220.

(3) 根据（1）（2）的结果可得：∠1＋∠2＝180°＋∠A

故答案是：∠1＋∠2＝180°＋∠A

练习册系列答案

（1）求证：∠EBD=∠CAB；

（2）若BC=，AC=5，求sin∠CBA．

【题目】如图，在平面直角坐标系中，的顶点在第一象限，点、的坐标分别为、，，，直线交轴于点，若与关于点成中心对称，则点的坐标为（）

A. B. C. D.

【题目】如图,AB=AC,∠BAC=90°,∠1=∠2,CE⊥BE.求证:BD=2CE.

【题目】如图，O为直线AB上一点，F为射线OC上一点，OE⊥AB．

（1）用量角器和直角三角尺画∠AOC的平分线OD，画FG⊥OC，FG交AB于点G；

（2）在（1）的条件下，比较OF与OG的大小，并说明理由；

（3）在（1）的条件下，若∠BOC＝40°，求∠AOD与∠DOE的度数．

【题目】把 6个相同的小正方体摆成如图的几何体．

（1）画出该几何体的主视图、左视图、俯视图；

（2）如果每个小正方体棱长为，则该几何体的表面积是．

（3）如果在这个几何体上再添加一些相同的小正方体，并并保持左视图和俯视图不变，那么最多可以再添加个小正方体．

【题目】在△ABC中，AB=AC，点D是射线CB上的一动点（不与点B、C重合），以AD为一边在AD的右侧作△ADE，使AD=AE，∠DAE=∠BAC，连接CE．

（1）如图1，当点D在线段CB上，且∠BAC=90°时，那么∠DCE= 度；

（2）设∠BAC= ，∠DCE= ．

① 如图2，当点D在线段CB上，∠BAC≠90°时，请你探究与之间的数量关系，并证明你的结论；

② 如图3，当点D在线段CB的延长线上，∠BAC≠90°时，请将图3补充完整，并直接写出此时与之间的数量关系（不需证明）．

【题目】如图，在矩形ABCD中，已知AB=8cm，BC=10cm，折叠矩形的一边AD，使点D落在BC边上的点F处，折痕为AE．以点A为原点，分别以AD所在的直线为x轴，AB所在的直线为y轴建立坐标系.

（1）写出点B、D、E、F的坐标；

（2）在坐标轴上是否存在点G，使△AFG是以AF为腰长的等腰三角形？若存在，请求出点G的坐标；若不存在，请说明理由.

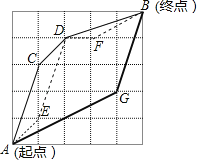
【题目】嘉嘉参加机器人设计活动，需操控机器人在5×5的方格棋盘上从A点行走至B点，且每个小方格皆为正方形，主办单位规定了三条行走路径R1，R2，R3，其行经位置如图与表所示：

路径	编号	图例	行径位置
第一条路径	R1	_	A→C→D→B
第二条路径	R2	…	A→E→D→F→B
第三条路径	R3	▂	A→G→B

已知A、B、C、D、E、F、G七点皆落在格线的交点上，且两点之间的路径皆为直线，在无法使用任何工具测量的条件下，请判断R1、R2、R3这三条路径中，最长与最短的路径分别为何？请写出你的答案，并完整说明理由．

试题分类