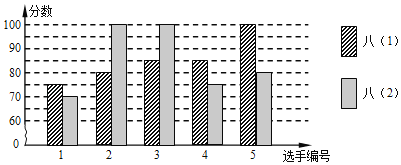
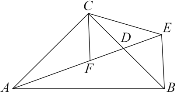
题目内容
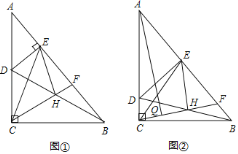
【题目】如图①，Rt△ABC中，∠ACB＝90°，点D为边AC上一点，DE⊥AB于点E，点H为BD中点，CH的延长线交AB于点F．
（1）求证：CH＝EH；
（2）若∠CAB＝40°，求∠EHF；
（3）如图②，若△DAE≌△CEH，点Q为CH的中点，连接AQ，求证：AQ∥EH．
【答案】（1）见解析；（2）∠EHF＝80°；（3）见解析
【解析】
（1）根据直角三角形斜边中线的性质证明即可．
（2）先根据等腰三角形的性质得：∠HCB＝∠HBC，∠HEB＝∠HBE，由三角形外角的性质得：∠DHC＝2∠HBC，∠DHE＝2∠HBE，从而有∠CHE＝2∠CBA，计算∠CBA＝50°，根据平角的定义可得结论；
（3）如图②，连接AH，先证明AE＝ED＝EH＝DH＝CH，得△DEH是等边三角形，所以∠DHC＝30°，∠AEH＝150°，再证明AC＝AH，根据等腰三角形三线合一可得AQ⊥CH，最后根据同位角相等，两直线平行可得结论．
（1）证明：如图①，∵DE⊥AB，
∴∠DEB＝90°，
在Rt△DEB和Rt△DCB中，∠DEB＝∠DCB＝90°，H为BD的中点，
∴EH＝
BD，CH＝BD，
∴EH＝CH；
（2）解：∵H为BD的中点，
∴BH＝BD，
∴BH＝EH＝CH，
∴∠HCB＝∠HBC，∠HEB＝∠HBE，
在△CHB和△EHB中，
∠DHC＝∠HCB+∠HBC，∠DHE＝∠HEB+∠HBE，
∴∠DHC＝2∠HBC，∠DHE＝2∠HBE，
∴∠CHE＝2∠CBA，
在Rt△ACB中，∠ACB＝90°，
∴∠A+∠CBA＝90°，
∵∠A＝40°，
∴∠CBA＝50°，
∴∠CHE＝100°，
∴∠EHF＝80°；
（3）证明：如图②，连接AH，
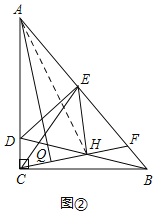
∵△DAE≌△CEH，
∴AE＝EH，∠AED＝∠EHC＝90°，
∵HC＝HE，DH＝BD，
∴AE＝ED＝EH＝DH＝CH，
∴△DEH是等边三角形，
∴∠DEH＝∠DHE＝60°，
∴∠DHC＝∠EHC﹣∠EHD＝30°，∠AEH＝∠AED+∠DEH＝150°，
∵AE＝EH，DH＝CH，
∴∠EHA＝（180°﹣∠AEH）÷2＝15°，
∠HCD＝（180°﹣∠DHC）÷2＝75°，
∴∠AHC＝∠EHC﹣∠EHA＝75°，
∴∠AHC＝∠ACH＝75°，
∴AC＝AH，
∵Q是CH的中点，
∴AQ⊥CH，
∴∠AQC＝90°，
∴∠AQC＝∠EHC，
∴AQ∥EH．
