题目内容
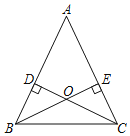
【题目】如图,正方形ABCD的边长为10,点E、F分别在边BC、CD上,且∠EAF=45°,AH⊥EF于点H,AH=10,连接BD,分别交AE、AH、AF于点P、G、Q.
(1)求△CEF的周长;
(2)若E是BC的中点,求证:CF=2DF;
(3)连接QE,求证:AQ=EQ.

【答案】(1)△ECF的周长为20;(2)证明见解析;(3)证明见解析.
【解析】
(1)想办法证明EB=EH,FD=FH,即可解决问题;
(2)通过计算求出CF、DF即可解决问题;
(3)想办法证明△APB∽△QPE,可得∠AEQ=∠ABP=45°即可解决问题.
(1)在Rt△ABE和Rt△AHE中,
∵∠ABE=∠AHE=90°,AB=AH=10,AE=AE,
∴△ABE≌△AHE,
∴BE=HE,同理,DF=FH,
∴△ECF的周长=CE+CF+EF=CE=CE+BE+CF+FD=CB+CD=20.
(2)∵E是BC中点,
∴BE=EC=EH=5,设DF=FH=x,则CF=10﹣x,
在Rt△ECF中,∵∠C=90°,
∴EF2=EC2+CF2,
∴52+(10﹣x)2=(5+x)2,
解得x=![]() ,即DF=
,即DF=![]() ,则CF=10﹣
,则CF=10﹣![]() =
=![]() ,
,
∴CF=2DF;
(3)在△BPE和△APQ中,∠EBP=∠QAP=45°,∠BPE=∠APQ,
∴△BPE∽△APQ,
∴![]() =
=![]() ,
,
即![]() =
=![]() ,
,
∵∠APB=∠QPE,
∴△APB∽△QPE,
∴∠QEP=∠ABP=45°,
∵∠EAF=45°,
∴∠QEA=∠QAE=45°,
∴AQ=EQ.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目