题目内容
【题目】已知抛物线y=ax2+3x+c(a,c为常数,且a≠0)经过点(﹣1,﹣1),(0,3),有下列结论:
①ac<0;
②当x>1时,y的值随x值的增大而减小;
③3是方程ax2+2x+c=0的一个根;
④当﹣1<x<3时,ax2+2x+c>0
其中正确结论的个数是( )
A.1B.2C.3D.4
【答案】C
【解析】
先由抛物线y=ax2+3x+c(a,c为常数,且a≠0)经过点(﹣1,﹣1),(0,3),列方程组求出a,c,从而解得其解析式,进而求得其对称轴,再根据二次函数与方程和二次函数与不等式的关系可解.
把点(﹣1,﹣1),(0,3)代入y=ax2+3x+c得:![]()
∴![]()
∴y=﹣x2+3x+3
∴①ac<0正确;
该抛物线的对称轴为:![]() ,
,
∴②当x>1时,y的值随x值的增大而减小是错误的;
方程ax2+2x+c=0可化为:方程ax2+3x+c=x,
把x=3代入y=﹣x2+3x+3得y=3,
∴﹣x2+2x+3=0,
故③正确;
∴(3,3)在该抛物线上,
又∵抛物线y=ax2+3x+c(a,c为常数,且a≠0)经过点(﹣1,﹣1),
∴抛物线y=ax2+3x+c与y=x的交点为(﹣1,﹣1)和(3,3),
当﹣1<x<3时,ax2+3x+c>x,即ax2+2x+c>0
④当﹣1<x<3时,ax2+2x+c>0,故④正确.
综上,①③④正确.
故选C.

 名师伴你成长课时同步学练测系列答案
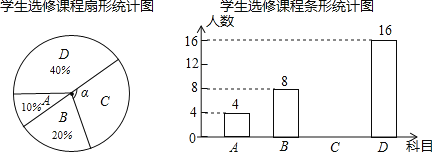
名师伴你成长课时同步学练测系列答案【题目】疫情期间,附中初![]() 级老师们为了解孩子们在家每周体育锻炼打卡情况,收集部分数据并绘制了如下尚不完整的参与打卡人数与坚持打卡天数的条形统计图和扇形统计图:
级老师们为了解孩子们在家每周体育锻炼打卡情况,收集部分数据并绘制了如下尚不完整的参与打卡人数与坚持打卡天数的条形统计图和扇形统计图:
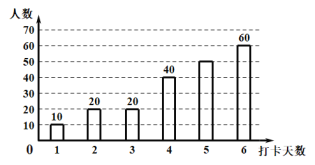
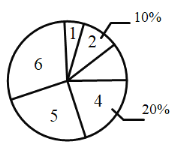
通过分析上面![]() 个统计图,制作如下表格:
个统计图,制作如下表格:
统计量 | 平均数 | 中位数 | 众数 |
天数 | 4.4 | a | b |
(1)填空:![]() _______,
_______,![]() _______,并补全条形统计图.
_______,并补全条形统计图.
(2)因为疫情期间,在家体育锻炼条件受限,所以规定坚持打卡不低于![]() 天即为合格.初
天即为合格.初![]() 级共有学生
级共有学生![]() 人,请你估计初
人,请你估计初![]() 级学生中体育锻炼合格的人数.
级学生中体育锻炼合格的人数.
(3)若统计时漏掉![]() 名学生,先将他的打卡天数和原统计的打卡天数合并成一组新数据后,发现平均数增大了,则漏掉的这名学生坚持打卡天数最少是多少天?
名学生,先将他的打卡天数和原统计的打卡天数合并成一组新数据后,发现平均数增大了,则漏掉的这名学生坚持打卡天数最少是多少天?