题目内容
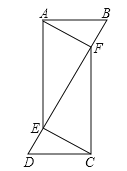
【题目】在△ABC中,D为AB的中点,F为BC上一点,DF∥AC,延长FD至E,且DE=DF,联结AE、AF

(1)求证:∠E=∠C;
(2)如果DF平分∠AFB,求证:AC⊥AB
【答案】(1)见解析;(2)见解析
【解析】
(1)根据SAS证明△AED与△BFD全等,再利用等量代换证明即可;
(2)根据角平分线的定义和等腰三角形的性质进行证明即可.
(1)∵D为AB的中点,
∴BD=AD,
在△AED与△BFD中,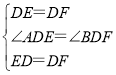 ,
,
∴△AED≌△BFD(SAS),
∴∠E=∠DFB,
∵DF∥AC,
∴∠C=∠DFB,
∴∠C=∠E;
(2)∵DF平分∠AFB,
∴∠AFD=∠DFB,
∵∠E=∠DFB,
∴∠AFD=∠AED,
∵ED=DF,
∴∠DAF+∠AFD=90°,
∵EF∥AC,
∴∠AFD=∠FAC,
∴∠DAF+∠FAC=90°,
∴AC⊥AB.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目