题目内容
【题目】转转盘和摸球是等可能概率下的经典模型.

(1)如图,转盘的白色扇形和黑色扇形的圆心角分别为120°和240°.小莉让转盘自由转动2次,求指针2次都落在黑色区域的概率.
(2)小刚在一个不透明的口袋中,放入除颜色外其余都相同的18个小球,其中4个白球,6个红球,8个黄球.搅匀后,随机摸1个球,若事件A的概率与(1)中概率相同,请写出事件A.
【答案】(1)![]() ;(2)事件A为摸得黄球.
;(2)事件A为摸得黄球.
【解析】
(1)抓住已知白色扇形和黑色扇形的圆心角分别为120°和240°,采用列举法,求出所有可能的结果数及指针2次都落在黑色区域的可能数,利用概率公式求解即可;
(2)分别求出摸出的球是白球、红球、黄球的概率,然后结合(1)中的概率即可写出事件A.
(1)如图,把黑色扇形等分为黑1、黑2两个扇形,
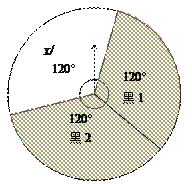
转盘自由转动2次,指针所指区域的结果如下:
(白,白),(白,黑1),(白,黑2),(黑1,白),(黑1,黑1),(黑1,黑2),
(黑2,白),(黑2,黑1),(黑2,黑2),
所有可能的结果共9种,它们是等可能的,其中指针2次都落在黑色区域的结果有4种,
所以P(指针2次都落在黑色区域)=![]() ;
;
(2)若摸出的球是白球,则概率为![]() ,
,
若摸出的球是红球,则概率为![]() ,
,
若摸出的球是黄球,则概率为![]() ,
,
所以事件A为摸得黄球.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目