题目内容
【题目】我们已经学习过:同弧或等弧所对的圆周角都相等,都等于该弧所对的圆心角的一半.请您就下面所给的图![]() 和图
和图![]() 中,圆心
中,圆心![]() 与
与![]() 的位置关系,证明:
的位置关系,证明:![]() .
.
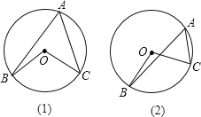
【答案】证明见解析
【解析】
(1)延长BO交⊙O于点D,连接CD,根据同弧或等弧所对的圆周角都相等可得∠A=∠D,再根据等腰三角形的两底角相等,∠D=∠OCD,然后利用三角形的外角性质∠BOC=∠D+∠OCD,整理即可得证;
(2)延长BO交⊙O于点E,连接CE,根据同弧或等弧所对的圆周角都相等可得∠A=∠E,再根据等腰三角形的两底角相等,∠E=∠OCE,然后利用三角形的外角性质∠BOC=∠E+∠OCE,整理即可得证;
![]() 如图
如图![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,则
,则
![]() (同弧或等弧所对的圆周角都相等),
(同弧或等弧所对的圆周角都相等),
∵![]() ,
,
∴![]() ,
,
∵![]() (三角形的一个外角等于与它不相等的两个内角的和),
(三角形的一个外角等于与它不相等的两个内角的和),
∴![]() ,
,
即![]() ;
;
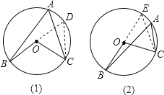
![]() 如图
如图![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,则
,则
![]() (同弧或等弧所对的圆周角都相等),
(同弧或等弧所对的圆周角都相等),
∵![]() ,
,
∴![]() ,
,
∵![]() (三角形的一个外角等于与它不相邻的两个内角的和),
(三角形的一个外角等于与它不相邻的两个内角的和),
∴![]() ,
,
即![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目