题目内容
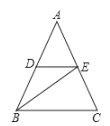
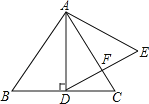
【题目】如图,在等边三角形ABC中,AD⊥BC于点D,BD=2,以AD为一边向右作等边三角形ADE.
(1)求△ABC的周长;
(2)判断AC、DE的位置关系,并给出证明.
【答案】(1)12;(2)AC⊥DE,理由见解析
【解析】
(1)根据等边三角形的性质求得BD=CD=2,即可求得BC=4,所以△ABC为边长为4的正三角形,从而求出三角形的周长;
(2)根据等边三角形的性质求得∠C=∠ADE=60°,再求出∠CDE=30°,从而得到∠CFD=90°即可得出结论.
解:(1)∵在等边△ABC中,AD⊥BC,BD=2,
∴BD=CD=2,
∴BC=BD+CD=4,
∴等边△ABC的周长为:AB+BC+CA=3BC=12;
(2)AC、DE的位置关系:AC⊥DE.
∵△ABC和△ADE是等边三角形,
∴∠C=60°,∠ADE=60°,
∵AD⊥BC,
∴∠ADC=90°,
在△CDF中,∵∠CDE=90°﹣∠ADE=30°,
∴∠CFD=180°﹣∠C﹣∠CDE=180°﹣60°﹣30°=90°.
∴AC⊥DE.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目