题目内容
如图，在菱形ABCD在，AE⊥BC，E为垂足，且BE=CE，AB=2．求：
（1）∠BAD的度数；
（2）对角线AC、BD的长．
（1）∠BAD的度数；
（2）对角线AC、BD的长．
（1）∵四边形ABCD是菱形，
∴AB=BC，
∵AE⊥BC，BE=CE，
∴AB=AC，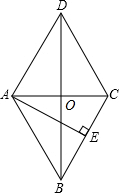
∴AB=BC=AC，
即△ABC是等边三角形，
∴∠BAC=60°，
∴∠BAD=2∠BAC=120°；
（2）∵四边形ABCD是菱形，
∴AC⊥BD，
∵AC=AB=2，
∴OA=
AC=1，
∴OB=
=
，
∴BD=2OB=2
；
∴AC=2，BD=2
．
∴AB=BC，
∵AE⊥BC，BE=CE，
∴AB=AC，
∴AB=BC=AC，
即△ABC是等边三角形，
∴∠BAC=60°，
∴∠BAD=2∠BAC=120°；
（2）∵四边形ABCD是菱形，
∴AC⊥BD，
∵AC=AB=2，
∴OA=
| 1 |
| 2 |
∴OB=
| AB2-OA2 |
| 3 |
∴BD=2OB=2
| 3 |
∴AC=2，BD=2
| 3 |
练习册系列答案
全能测控一本好卷系列答案
发散思维新课堂系列答案
相关题目
