题目内容
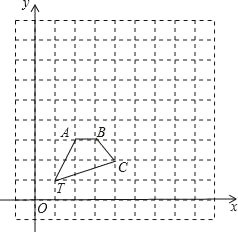
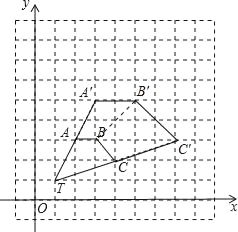
【题目】如图,在正方形网格中,四边形TABC的顶点坐标分别为T(1,1),A(2,3),B(3,3),C(4,2).
(1)以点T(1,1)为位似中心,在位似中心的同侧将四边形TABC放大为原来的2倍,放大后点A,B,C的对应点分别为A′,B′,C′画出四边形TA′B′C′;
(2)写出点A′,B′,C′的坐标:
A′ ,B′ ,C′ ;
(3)在(1)中,若D(a,b)为线段AC上任一点,则变化后点D的对应点D′的坐标为 .
【答案】(1)详见解析;(2)A′(3,5),B′(5,5),C′(7,3);(3)点D′的坐标为(2a﹣1,2b﹣1).
【解析】
(1)利用位似图形的性质得出变化后图形即可;
(2)利用已知图形得出对应点坐标;
(3)利用各点变化规律,进而得出答案.
(1)如图所示:四边形TA′B′C′即为所求;
(2)A′(3,5),B′(5,5),C′(7,3);
故答案为:(3,5),(5,5),(7,3);
(3)在(1)中,∵A(2,3),B(3,3),C(4,2),
A′(2×2﹣1=3,2×3﹣1=5),B′(2×3﹣1=5,2×3﹣1=5),C′(2×4﹣1=7,2×2﹣1=3);
∴D(a,b)为线段AC上任一点,
则变化后点D的对应点D′的坐标为(2a﹣1,2b﹣1).
故答案为:(2a﹣1,2b﹣1).

练习册系列答案
相关题目