题目内容
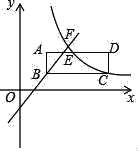
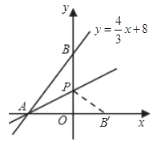
【题目】如图,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,点
,点![]() ,
,![]() 是
是![]() 上的一点,若将
上的一点,若将![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 恰好落在
恰好落在![]() 轴上的点
轴上的点![]() 处,则直线
处,则直线![]() 的表达式是_________.
的表达式是_________.
【答案】y=![]() x+3.
x+3.
【解析】
由直线![]() 即可得到A(-6,0),B(0,8),再根据勾股定理即可得到P(0,3),利用待定系数法即可得到直线AP的表达式.
即可得到A(-6,0),B(0,8),再根据勾股定理即可得到P(0,3),利用待定系数法即可得到直线AP的表达式.
令![]() ,则
,则![]() ,令
,令![]() ,则
,则![]() ,
,
由直线![]() 与
与![]() 轴,
轴,![]() 轴交点坐标为:A(-6,0),B(0,8),
轴交点坐标为:A(-6,0),B(0,8),
∴AO=6,BO=8,
∴![]() ,
,
由折叠可得AB'=AB=10,B'P=BP,
∴OB'= AB'- AO ![]() ,
,
设P(0,![]() ),则OP=y,B'P=BP=
),则OP=y,B'P=BP=![]() ,
,
∵Rt△POB'中,PO2+B'O2=B'P2,
∴y2+42=(![]() )2,
)2,
解得:![]() ,
,
∴P(0,3),
设直线AP的表达式为![]() ,
,
则![]() ,
,
![]() ,
,
∴直线AP的表达式是![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目