题目内容
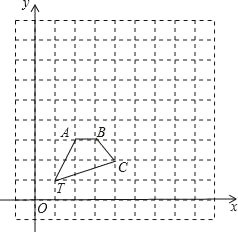
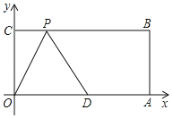
【题目】如图，在平面直角坐标系中，O为坐标原点，四边形OABC是长方形，点A、C的坐标分别为A（10，0）、C（0，4），点D是OA的中点，点P在BC边上运动，当△ADP为等腰三角形时，点P的坐标为_______________________________．
【答案】(2，4)，(8，4)，(7，4)，(7.5，4)
【解析】
分PD=DA，AD=PA，DP=PA三种情况讨论，再根据勾股定理求P点坐标
当PD=DA
如图：以D为圆心AD长为半径作圆，与BD交P点，P'点，过P点作PE⊥OA于E点，过P'点作P'F⊥OA于F点，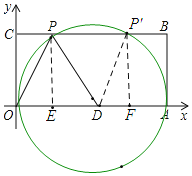
∵四边形OABC是长方形，点A、C的坐标分别为A（10，0）、C（0，4），
∴AD=PD=5，PE=P'F=4
∴根据勾股定理得：DE=DF=
∴P（2，4），P'（8，4）
若AD=AP=5，同理可得：P（7，4）
若PD=PA，则P在AD的垂直平分线上，
∴P（7.5，4）
故答案为：（2，4），（8，4），（7，4），（7.5，4）
练习册系列答案
名牌学校分层周周测系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
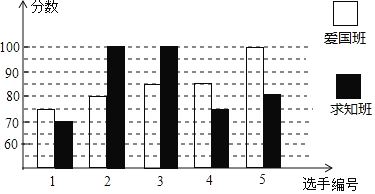
【题目】某校初二开展英语拼写大赛，爱国班和求知班根据初赛成绩，各选出5名选手参加复赛，两个班各选出的5名选手的复赛成绩如图所示：
（1）根据图示填写下表：
班级 | 中位数（分） | 众数（分） | 平均数（分） |
爱国班 | 85 | ||
求知班 | 100 | 85 |
（2）结合两班复赛成绩的平均数和中位数，分析哪个班级的复赛成绩比较好？
（3）已知爱国班复赛成绩的方差是70，请求出求知班复赛成绩的方差，并说明哪个班成绩比较稳定？
