题目内容
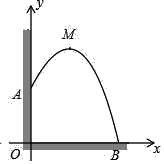
【题目】从某幢建筑物10m高的窗口A处用水管向外喷水，喷出的水成抛物线状（抛物线所在平面与地面垂直）．抛物线的最高点M离墙1m，离地面
m．
(1)建立适当的平面直角坐标系，求抛物线的解析式．
(2)求水的落地点B与点O的距离．
【答案】(1)y=﹣
（x﹣1）2+
；(2)水的落地点B与点O距离为3米．
【解析】
根据题意得出二次函数顶点坐标为M（1，），设出顶点式，代入点A（0，10）进而求出抛物线解析式；
（2）令y=0时，解一元二次方程即可，在实际问题中，注意负值舍去．
．解：（1）建立如图所示的平面直角坐标系，则A（0，10），
由题意得M（1，
），
设该抛物线的解析式为：y=a（x﹣1）2+，
将A（0，10）代入，得10=a+，
解得：a=﹣，
∴y=﹣ （x﹣1）2+ ；
（2）当y=0时，﹣（x﹣1）2+=0，
解得：x1=3，x2=﹣1，
∴OB=3，水的落地点B与点O距离为3米．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
