题目内容
【题目】如图,![]() 与
与![]() 在线段
在线段![]() 的同侧,
的同侧,![]() ,
,![]() .
.
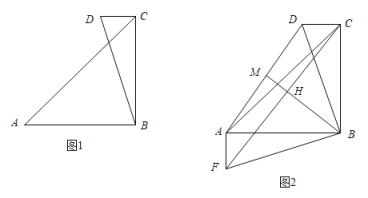
(1)如图![]() ,已知
,已知![]() ,
,![]() ,求
,求![]() 的长;
的长;
(2)如图![]() ,将
,将![]() 绕着点
绕着点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,点
,点![]() 、
、![]() 的对应点分别是点
的对应点分别是点![]() 、
、![]() ,连接
,连接![]() 和
和![]() .过点
.过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() ;(2)详见解析.
;(2)详见解析.
【解析】
(1)在Rt△ABC中,利用特殊角的三角函数值求得BC的长,然后在Rt△BCD中,利用勾股定理即可求得答案;
(2)先根据旋转的性质得到∠AFB=∠BDC,∠FAB=∠DCB=90°,BF=BD,BC=AB,进而推出AF∥BC,再根据平行线的性质的性质得到∠FBC =∠BDQ,则通过“角角边”证明△FBC≌△BDQ,得到FC=BQ,BC=DQ,再通过“角角边”证明△ABM≌△DQM,得到BM=MQ=![]() BQ=
BQ=![]() FC,即可得证.
FC,即可得证.
解(1)∵△ABC为直角三角形,且AB=BC,
∴△ABC为等腰直角三角形,
∴BC=AC·sin45°=6![]() ·
·![]() =6,
=6,
在Rt△BCD中,
CD=![]() =
=![]() =
=![]() ;
;
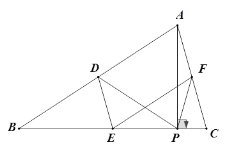
(2)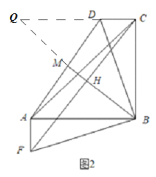
如图,分别延长BM、CD交于点Q,
∵∠BCQ=90°,BH⊥EC,
∴∠Q=∠BCH,
又∵将![]() 绕着点
绕着点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() ,
,
∴∠AFB=∠BDC,∠FAB=∠DCB=90°,BF=BD,BC=AB,
∵∠ABC=90°,
∴AF∥BC,
∴∠FBC=180°﹣∠AFB=180°﹣∠BDC=∠BDQ,
∴△FBC≌△BDQ(AAS),
∴FC=BQ,BC=DQ,
∵BC=AB,
∴DQ=AB,
∵AB∥CD,
∴∠BAD=∠QDA,
∴△ABM≌△DQM(AAS),
∴BM=MQ=![]() BQ=
BQ=![]() FC,
FC,
∴CF=2BM.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目