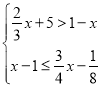��Ŀ����
����Ŀ����֪�ڱ߳�Ϊ4������ABCD�У���EBF=��A=60�㣬
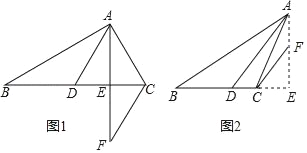
��1����ͼ�٣�����E��F�ֱ����߶�AD��DC�ϣ�
���жϡ�EBF����״����˵�����ɣ�
�����ı���ABFD�����Ϊ7![]() ����DE�ij���
����DE�ij���
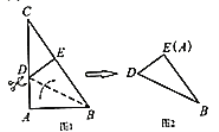
��2����ͼ�ڣ�����E��F�ֱ����߶�AD��DC���ӳ����ϣ�BE��DC���ڵ�O�����BOF�����ΪS1����EOD�����ΪS2����S1-S2��ֵ�Ƿ�Ϊ��ֵ������ǣ��������ֵ��������ǣ���˵�����ɣ�
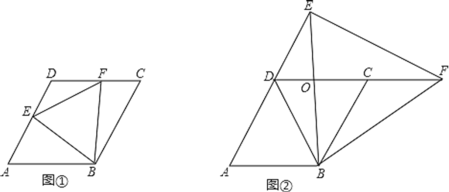
���𰸡���1���١�EBF�ǵȱ������Σ�����������DE=1����2��S1-S2��ֵ�Ƕ�ֵ��S1-S2=4![]() ��
��
��������
��1���١�EBF�ǵȱ������Σ�����BD��֤����ABE�ա�DBF��ASA�����ɽ�����⣮
����ͼ1�У���BH��AD��H�������ABE����������������ε������ʽ���AE���ɽ�����⣮
��2����ͼ2�У����ۣ�S1-S2��ֵ�Ƕ�ֵ����취֤����S1-S2=S��BCD���ɣ�
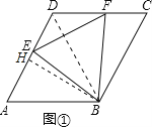
�⣺��1���١�EBF�ǵȱ������Σ��������£�
��ͼ1�У�����BD��
���ı���ABCD�����Σ�
��AD=AB��
�ߡ�ADB=60����
���ADB�ǵȱ������Σ���BDC�ǵȱ������Σ�
��AB=BD����ABD=��A=��BDC=60����
�ߡ�ABD=��EBF=60����
���ABE=��DBF��
����ABE����DBF��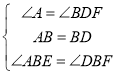 ��
��
���ABE�ա�DBF��ASA����
��BE=BF��
�ߡ�EBF=60����
���EBF�ǵȱ������Σ�
����ͼ1�У���BH��AD��H��
��Rt��ABH��BH=2![]() ��
��
��S��ABD=![]() ADBH=4
ADBH=4![]() ��
��
��S�ı���ABFD=7![]() ��
��
��S��BDF=S��ABE=3![]() ��
��
��![]() =3
=3![]() ��
��
��AE=3��
��DE=AD=AE=1��
��2����ͼ2�У����ۣ�S1-S2��ֵ�Ƕ�ֵ��
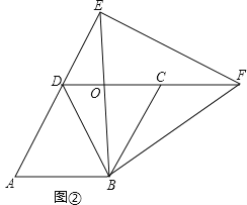
���ɣ��ߡ�BDC����EBF���ǵȱ������Σ�
��BD=BC����DBC=��EBF=60����BE=BF��
���DBE=��CBF��
���DBE�ա�CBF��SAS����
��S��BDE=S��BCF��
��S1-S2=S��BDE+S��BOC-S��DOE=S��DOE+S��BOD+S��BOC-S��DOE=S��BCD=![]() ��42=4
��42=4![]() ��
��
��S1-S2��ֵ�Ƕ�ֵ��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�