题目内容
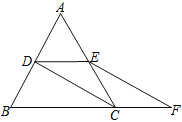
【题目】已知四边形ABCD中,AB=AD,AB⊥AD,连接AC,过点A作AE⊥AC,且使AE=AC,连接BE,过A作AH⊥CD于H交BE于F.

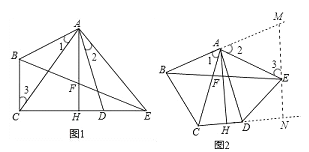
(1)如图1,当E在CD的延长线上时,求证:①△ABC≌△ADE;②BF=EF;
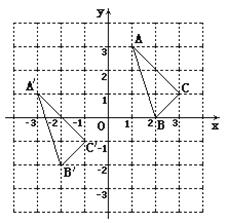
(2)如图2,当E不在CD的延长线上时,BF=EF还成立吗?请证明你的结论.
【答案】(1)详见解析;(2)结论仍然成立,理由详见解析.
【解析】
试题分析:(1)①根据已知条件,利用SAS即可判定△ABC≌△ADE;②易证BC∥FH和CH=HE,根据平行线分线段成比例定理可证得BF=EF.(2)过E作MN⊥AH,交BA、CD延长线于M、N,,利用ASA证明△MAE≌△DAC,得AD=AM,根据等量代换得AB=AM,根据②同理得出结论.
试题解析:证明:(1)①如图1,
∵AB⊥AD,AE⊥AC,
∴∠BAD=90°,∠CAE=90°,
∴∠1=∠2,
在△ABC和△ADE中,
∵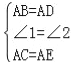
∴△ABC≌△ADE(SAS);
②如图1,
∵△ABC≌△ADE,
∴∠AEC=∠3,
在Rt△ACE中,∠ACE+∠AEC=90°,
∴∠BCE=90°,
∵AH⊥CD,AE=AC,
∴CH=HE,
∵∠AHE=∠BCE=90°,
∴BC∥FH,
∴![]() =1,
=1,
∴BF=EF;
(2)结论仍然成立,理由是:
如图2所示,过E作MN⊥AH,交BA、CD延长线于M、N,
∵∠CAE=90°,∠BAD=90°,
∴∠1+∠2=90°,∠1+∠CAD=90°,
∴∠2=∠CAD,
∵MN∥AH,
∴∠3=∠HAE,
∵∠ACH+∠CAH=90°,∠CAH+∠HAE=90°,
∴∠ACH=∠HAE,
∴∠3=∠ACH,
在△MAE和△DAC中,
∵
∴△MAE≌△DAC(ASA),
∴AM=AD,
∵AB=AD,
∴AB=AM,
∵AF∥ME,
∴![]() =1,
=1,
∴BF=EF.