Question

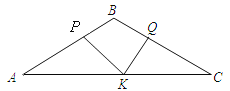
【题目】如图，在△ABC中，AB＝BC＝4，S△ABC＝4，点P、Q、K分别为线段AB、BC、AC上任意一点，则PK＋QK的最小值为_______

Answer 1

【答案】2

【解析】试题解析：：如图，过A作AH⊥BC交CB的延长线于H，

∵AB=CB=4，S△ABC=4，

∴AH=2，

∴cos∠HAB=，

∴∠HAB=30°，

∴∠ABH=60°，

∴∠ABC=120°，

∵∠BAC=∠C=30°，

作点P关于直线AC的对称点P′，

过P′作P′Q⊥BC于Q交AC于K，

则P′Q 的长度=PK+QK的最小值，

∴∠P′AK=∠BAC=30°，

∴∠HAP′=90°，

∴∠H=∠HAP′=∠P′QH=90°，

∴四边形AP′QH是矩形，

∴P′Q=AH=2，

即PK+QK的最小值为2．