题目内容
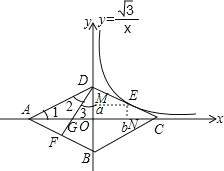
【题目】已知,如图2菱形ABCD四个顶点都在坐标轴上,对角线AC、BD交于原点O,DF垂直AB交AC于点G,反比例函数![]() ,经过线段DC的中点E,若BD=4,则AG的长为( )
,经过线段DC的中点E,若BD=4,则AG的长为( )

A.![]() B.
B.![]() +2 C.2
+2 C.2![]() +1 D.
+1 D.![]() +1
+1
【答案】A.
【解析】
试题解析:过E作y轴和x的垂线EM,EN,
设E(b,a),
∵反比例函数![]() 经过点E,
经过点E,
∴ab=![]() ,
,
∵四边形ABCD是菱形,
∴BD⊥AC,DO=![]() BD=2,
BD=2,
∵EN⊥x,EM⊥y,
∴四边形MENO是矩形,
∴ME∥x,EN∥y,
∵E为CD的中点,
∴DOCO=4![]() ,
,
∴CO=2![]() ,
,
∴tan∠DCO=![]() ,
,
∴∠DCO=30°,
∵四边形ABCD是菱形,
∴∠DAB=∠DCB=2∠DCO=60°,∠1=30°,AO=CO=2![]() ,
,
∵DF⊥AB,
∴∠2=30°,
∴DG=AG,
设DG=r,则AG=r,GO=2![]() -r,
-r,
∵AD=AB,∠DAB=60°,
∴△ABD是等边三角形,
∴∠ADB=60°,
∴∠3=30°,
在Rt△DOG中,DG2=GO2+DO2,
∴r2=(2![]() -r)2+22,
-r)2+22,
解得:r=![]() ,
,
∴AG=![]() ,
,
故选A.

练习册系列答案
相关题目

