äãá¢áÖàï
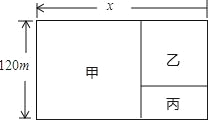
Àƒäãá¢À¢Ø£¡—ÅÀñÓµïÆŠØ£¡—ǵñÓçàÅöæÇëõà¨üÁë˜È˜ù■ûúçáÅöæÇàÓë¥ùªòƒÈ˜óðøÅÑå§úüÔACÀëBDÈÛØîøˆù■ûúçáÑåÆÎÝÔøÛÝàöˆ1Ȥ3ȘÅÀñÓµïê§ä¾Ñå§úüÔçá°Êñøeöˆ12cm¤ë14cmÈÛ

È´1ÈˋÅÀñÓµïçáûÌ£»òúÑÁèìÈ¢
È´2ÈˋàÓ¿«åÖǵñÓµïáÖæ¯èÒØ£¡—꘧ÆÑå§úÑËçÐçáòÛæø§£ýÌÅöçáøÏ°é¥ÉȘáúûÇøêèìÅÒÆûÑÁ°ÊçáýáêüȢȴý£¥úùÞ¤áÈˋ
È´3ÈˋǵñÓµï؈Æûýòè¨ø§¡ý¡úȘѽýòè¨ø§òúÇÆØ£íé¡í¤û¡ý¡úí«¡—ñÓµïçáƒÄÅöýòè¨ø§È´àÓë¥øÅÅÕüÔùªòƒÈˋýû¥¶üôâÇçáȘáúûÇÇÆùá¡—§úýû¥¶üôâÇñüóºý£Æûçáýòè¨ø§çáûÌ£»òúÑÁèìÈ¢
ÀƒÇÞ¯¡À¢(1)84È´cmÈˋ2;(2) 78cm;(3) 756È´cmÈˋ2
Àƒ§ãö—À¢
È´1Èˋ¡ªƒï໧úÅöçáûÌ£»¿¨ò§êÅò§¥óùХǢèÈ£
È´2Èˋ¡ªƒïüÁùó໧úÅöçáÅåøòçûç§AÀðCÀð=3AC=42cmȘë˜âÚBÀðDÀð=3BD=36cmȘÆÖòúçû秧ÃôÜÈ£
È´3Èˋ¡ªƒïƒÄÅö¤ë໧úÅöçáûÌ£»¿¨ò§¥Ç¢èçû秧ÃôÜÈÛ
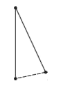
§ãȤȴ1ÈˋÀÔACÀëBDȘ
ÀÁÅÀñÓµïçáûÌ£»Sȧ![]() ACBDȧ
ACBDȧ![]() Àê12Àê14ȧ84È´cmÈˋ2È£
Àê12Àê14ȧ84È´cmÈˋ2È£
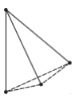
È´2ÈˋÀÔÅÀñÓµïƊǵñÓµïÅöæÇëõà¨üÁë˜È˜
ÀÁ¥ìèÒǵñÓµïçáùá¡—ÑËçÐöˆAÀðȘBÀðȘCÀðȘDÀðȘ
ÀÁÀ¼ABCDÀæÀ¼AÀðBÀðCÀðDÀðȘ
ÀÔù■ûúçáÑåÆÎÝÔøÛÝàöˆ1Ȥ3Ș
ÀÁAÀðCÀðȧ3ACȧ42cmȘ
ë˜âÚBÀðDÀðȧ3BDȧ36cmȘ
ÀÁøêèìÅÒÆû42+36ȧ78cmçáýáêüÈ£
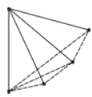
È´3ÈˋÇÆùá¡—§úýû¥¶üôâÇñüóºý£Æûçáýòè¨ø§çáûÌ£»È§ƒÄÅöçáûÌ£»ˋǵñÓµïçáûÌ£»È§42Àê36ˋ9Àê84ȧ756È´cmÈˋ2ÈÛ

Àƒäãá¢À¢åáÑêüôûÌáÖàïȘý¯Ç؈úµ§ãƒ—öòäãȤ
öòäãȤÀ¯åÖó§ûÌáÖȘØîøˆñøÝÞÆÅ2¡—çÐȘ3¡—çÐȘ4¡—çÐȘ5¡—çÐȘÀÙȘ![]() ¡—çÐȘóðøÅàöØã໡—çÐÑ¥ý£åÖë˜Ø£ä¾øÝüÔèüƒÙ¿»û¢ê§çУÙØ£ä¾øÝüÔȘù■ûú¢èØåñøÝÞ£ÙÑÁèìä¾øÝüÔÈ¢ÀÝ
¡—çÐȘóðøÅàöØã໡—çÐÑ¥ý£åÖë˜Ø£ä¾øÝüÔèüƒÙ¿»û¢ê§çУÙØ£ä¾øÝüÔȘù■ûú¢èØåñøÝÞ£ÙÑÁèìä¾øÝüÔÈ¢ÀÝ
䧃¢È¤öˆêù§ãƒ—íã¡—öòäãȘüÈë«ÅÀæÕçáë˜îÏûúȘèÒ¥óêùàÓüôÝÚ¡þ§½ÅÅ䧃¢È¤È´öˆêùñ§ÝÐîŃ¢öòäãȘë¥øÅû¢ä¾üÔÑöÝÚòƒ¿»üÔÑöê§ÑùçÐçáØ£ä¾øÝüÔÈˋ
çÐò» | 2 | 3 | 4 | 5 | ÀÙ |
|
òƒØãë¥ |
|
|
|
| ÀÙ |
|
øÝüÔä¾ò» | 1 |
|
|
| ÀÙ |
úŠ§ãÇÞüôêÅöòäãȤ
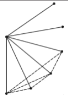
È´1ÈˋúŠ¯ÿøºüÈë«ÅÀæÕ¿ÕáèȘýÂøݧÆÅÇ°—§ÃôÜȤçÝó§ûÌáÖÆÅ![]() ¡—çÐòÝȘøÝüÔä¾ò»öˆ______È£
¡—çÐòÝȘøÝüÔä¾ò»öˆ______È£
È´2Èˋà¶á°ë˜îϯÇíí݃äãøÅçáñ§ñ´È˜¿ý£Ùêù28ä¾øÝüÔȘúµ¡ûó§ûÌáÖÆÅÑÁèì¡—ØîøˆçÐÈ¢
Àƒäãá¢À¢À¯öÍØ£ÀÝú¯üÎȘᰃÙüºèä¥ó£Û£´23500刿¤ô·AÀÂBÀÂCà»øøÅô¢ŸòÝ毿ý50ä槽ÅÅòåüºÈ˜ýÂúØ¿¤§½çáCøøòÝæ¯äæò»ý£èìÆÖBøøòÝæ¯äæò»È˜úØý£°˜¿»AøøòÝæ¯äæò»È˜èÒ¿¤§½AøøòÝæ¯xäæȘBøøòÝæ¯yäæȘà»øøòÝæ¯ç᧽¥Ü¤ëòÜ¥ÜàÓüôÝÚùªòƒÈÛ
Åë¤é | A | B | C |
§½¥ÜÈ´åˆ/äæÈˋ | 400 | 550 | 500 |
òÜ¥ÜÈ´åˆ/äæÈˋ | 500 | 700 | 650 |
È´1ÈˋúµyÆŠxøÛ¥ðçá¤₤ò»¿Äüçò§È£
È´2ÈˋôºæÐä¾¥±ç᧽£¾ñ§¯¡ÆÅáᥡøøÈ¢ÅÇ°—§ãÇÞ¿»°äÈ£
È´3Èˋ¥ìèÒùª¿¤§½çáíãà»øøòÝæ¯áÉà¨ý¢ô¶°—ȘúØåÖ¿¤üºíãéºòÝæ¯çá¿»°äøÅÅÒ؈êÚëãøÏ°—¡¼øøñîÆû1000åˆÈÛë´¿»¥óùÐéÅÑüááøø§½£¾ñ§¯¡â«àµæŸÇµÈÛ