题目内容
【题目】阅读下面内容，并按要求解决问题：
问题：“在平面内，已知分别有2个点，3个点，4个点，5个点，…，
个点，其中任意三个点都不在同一条直线上经过每两点画一条直线，它们可以分别画多少条直线？”
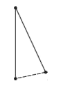
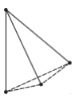
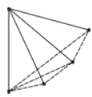
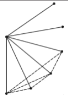
探究：为了解决这个问题，希望小组的同学们，设计了如下表格进行探究：（为了方便研究问题，图中每条线段表示过线段两端点的一条直线）
点数 | 2 | 3 | 4 | 5 | … |
|
示意图 |
|
|
|
| … |
|
直线条数 | 1 |
|
|
| … |
请解答下列问题：
（1）请帮助希望小组归纳，并直接写出结论：当平面内有个点时，直线条数为______；
（2）若某同学按照本题中的方法，共画了28条直线，求该平面内有多少个已知点？
【答案】（1）
；（2）该平面内有8个已知点．
【解析】
（1）根据图表中数据过两点的直线有1条，过不在同一直线上的三点的直线有3条，过任何三点都不在一条直线上的四点的直线有6条，可总结归纳出平面内点与直线的关系为；
（2）设设该平面内有
个已知点．利用得出的关系式列方程求解即可．
解：（1）当平面内有2个点时：可以画 
条直线；
当平面内有3个点时：可以画 
条直线；
当平面内有4个点时：可以画 
条直线；
…
当平面内有
个点时：可以画 
条直线；
（2）设该平面内有个已知点．
由题意，得
．
解得
，
（舍）．
答：该平面内有8个已知点．
备战中考寒假系列答案
【题目】为了解某区八年级学生的睡眠情况，随机抽取了该区八年级学生部分学生进行调查.已知D组的学生有15人，利用抽样所得的数据绘制所示的统计图表.
一、学生睡眠情况分组表（单位：小时）
组别 | 睡眠时间 |
|
|
|
|
|
|
|
|
|
|
二、学生睡眠情况统计图
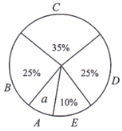
根据图表提供的信息，回答下列问题：
（1）试求“八年级学生睡眠情况统计图”中的a的值及a对应的扇形的圆心角度数；
（2）如果睡眠时间x（时）满足：
，称睡眠时间合格.已知该区八年级学生有3250人，试估计该区八年级学生睡眠时间合格的共有多少人？
（3）如果将各组别学生睡眠情况分组的最小值（如C组别中，取
），B、C、D三组学生的平均睡眠时间作为八年级学生的睡眠时间的依据.试求该区八年级学生的平均睡眠时间.
