Question

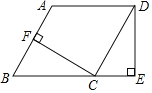
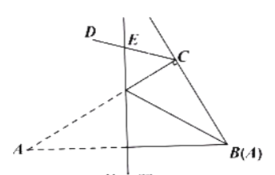
【题目】如图所示，在中，，将折叠，使点落在点处，折痕所在直线交的外角平分线于点，则点到的距离为______．

Answer 1

【答案】

【解析】

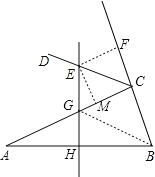
连接GB，作EF⊥BC于F，EM⊥AC于M，就可以得出EM=EF，设AG=y，则BG=y，GC=10-y．在Rt△GCB中，由勾股定理求出y的值，得到CG的长．设EF=x，则EM=MC=x，GM=GC-MC=．通过证明△GEM∽△CAB，得到，代入即可求出结论．

连接GB，作EF⊥BC于F，EM⊥AC于M，

∴∠EMC=∠EMG=∠EFC=90°．

∵CD平分∠ACF，

∴EM=EF，∠ACD∠ACF．

∵∠ACB=90°，

∴∠ACF=90°，

∴∠ACD=45°，

∴∠CEM=45°，

∴∠CEM=∠ECM，

∴EM=MC．

设AG=y，则BG=y，GC=10-y．在Rt△GCB中，∵，

∴，解得：y=，

∴CG=10-y=．

设EF=x，则EM=MC=x，GM=GC-MC=．

∵△AGH与△BGH关于GH对称，

∴AHAB，AG=GB，∠AHG=∠BHG=90°．

∵∠ACB=90°，

∴∠EMG=∠ACB=90°，

∴∠MEG+∠MGE=90°，∠AGH+∠A=90°．

∵∠EGM=∠AGH，

∴∠A=∠MEG，

∴△GEM∽△BAC，

∴，

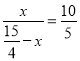∴，解得：x=．

故答案为：．