Question

【题目】“五一”前夕，某经销商计划花23500元购买A、B、C三种新款时装共50套进行试销，并且购进的C种时装套数不少于B种时装套数，且不超过A种时装套数，设购进A种时装x套，B种时装y套，三种时装的进价和售价如下表所示．

型号	A	B	C
进价（元/套）	400	550	500
售价（元/套）	500	700	650

（1）求y与x之间的函数关系式；

（2）满足条件的进货方案有哪几种？写出解答过程；

（3）假设所购进的这三种时装能全部卖出，且在购销这批时装的过程中需要另外支出各种费用1000元．通过计算判断哪种进货方案利润最大．

Answer 1

【答案】（1）y=2x﹣30；（2）有三种进货方案：方案一：进A种20套，B种10套，C种20套；方案二：进A种21套，B种12套，C种17套；方案三：进A种22套，B种14套，C种14套；（3）按（2）中方案一进货利润最大．

【解析】

（1）根据题意可得购进C种时装(50﹣x﹣y)套，利用“经销商计划花23500元购买A、B、C三种新款时装”进一步列出化简即可；

（2）根据题意求出符合题意得x的范围，进而求出方案；

（3）根据图表求出利润关于x的解析式，然后利用函数的增减性进一步判断即可.

（1）由题意知，购进C种时装(50﹣x﹣y)套，

400x+550y+500(50﹣x﹣y)=23500，

整理，得y=2x﹣30，

（2）由（1）知50﹣x﹣y=50﹣x﹣(2x﹣30)=﹣3x+80，

根据题意，得：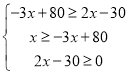

∴20≤x≤22．

∵x为整数，∴x可取20或21或22，∴有三种进货方案

方案一：进A种20套，B种10套，C种20套；

方案二：进A种21套，B种12套，C种17套；

方案三：进A种22套，B种14套，C种14套，

（3）设利润为w元，则

w=500x+700(2x﹣30)+650(﹣3x+80)﹣23500﹣1000=﹣50x+6500．

∵﹣50＜0，

∴w随x的增大而减小，

∴当x=20时w最大，

∴按（2）中方案一进货利润最大．