Question

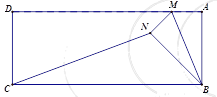
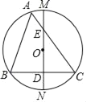
【题目】如图，△ABC内接于⊙O，AB＝BC，直径MN⊥BC于点D，与AC边相交于点E，若⊙O的半径为2，OE＝2，则OD的长为_____．

Answer 1

【答案】2

【解析】

连接BO并延长交AC于F，如图，先利用垂径定理得到BF⊥AC，BD=CD，再证明Rt△BOD∽Rt△EOF得到, 则设OF=x，则OD=x, 接着证明Rt△DBO∽Rt△DEC，利用相似比得到, 所以DB2=3x2+2x然后利用勾股定理得到关于x的方程，最后解方程求出x后，计算x即可．

解：连接BO并延长交AC于F，如图，

∵BA＝BC，

∴，

∴BF⊥AC，

∵直径MN⊥BC，

∴BD＝CD，

∵∠BOD＝∠EOF，

∴Rt△BOD∽Rt△EOF，

∴，

设OF＝x，则OD＝x，

∵∠DBO＝∠DEC，

∴Rt△DBO∽Rt△DEC，

∴，即，

而BD＝CD，

∴x，

在Rt△OBD中，，解得（舍去），

∴OD＝x＝2．

故答案为2．