Question

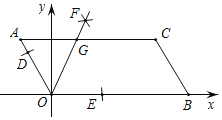
【题目】如图，已知AOBC的顶点O（0，0），A（﹣1，2），点B在x轴正半轴上按以下步骤作图：①以点O为圆心，适当长度为半径作弧，分别交边OA，OB于点D，E；②分别以点D，E为圆心，大于DE的长为半径作弧，两弧在∠AOB内交于点F；③作射线OF，交边AC于点G，则点G的坐标为（　　）

A. （﹣1，2） B. （，2） C. （3﹣，2） D. （﹣2，2）

Answer 1

【答案】A

【解析】依据勾股定理即可得到Rt△AOH中，AO=，依据∠AGO=∠AOG，即可得到AG=AO=，进而得出HG=-1，可得G（-1，2）．

如图，过点A作AH⊥x轴于H，AG与y轴交于点M，

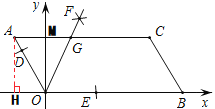
∵AOBC的顶点O（0，0），A（-1，2），

∴AH=2，HO=1，

∴Rt△AOH中，AO=，

由题可得，OF平分∠AOB，

∴∠AOG=∠EOG，

又∵AG∥OE，

∴∠AGO=∠EOG，

∴∠AGO=∠AOG，

∴AG=AO=，

∴MG=-1，

∴G（-1，2），

故选：A．