题目内容
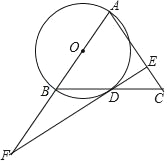
【题目】如图,在等腰△ABC中,AB=AC,以AB为直径作⊙O交边BC于点D,过点D作DE⊥AC交AC于点E,延长ED交AB的延长线于点F.
(1)求证:DE是⊙O的切线;
(2)若AB=8,AE=6,求BF的长.
【答案】(1)证明见解析;(2)4
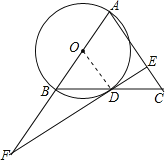
【解析】分析:(1)连接OD,根据等腰三角形的性质得到∠ABC=∠C,∠ABC=∠ODB,证明OD∥AC,根据平行线的性质得到OD⊥DE,根据切线的判定定理证明;
(2)证明△FOD∽△FAE,根据相似三角形的性质定理列出比例式,计算即可.
详(1)证明:连接OD,
∵AB=AC,
∴∠ABC=∠C,
∵OB=OD,
∴∠ABC=∠ODB,
∴∠ODB=∠C,
∴OD∥AC,又DE⊥AC,
∴OD⊥DE,
∴DE是⊙O的切线;
(2)解:∵OD∥AC,
∴△FOD∽△FAE,
∴![]() ,即
,即![]() ,
,
解得,BF=4.

【题目】据《南昌晚报》2019 年 4 月 28 日报道,“五一”期间南昌天气预报气温如下:
时间 | 4 月 29 日 | 4 月 30 日 | 5 月 1 日 | 5 月 2 日 | 5 月 3 日 |
最低气温 | 18℃ | 18℃ | 19℃ | 18℃ | 19℃ |
最高气温 | 22℃ | 24℃ | 27℃ | 22℃ | 24℃ |
则“五一”期间南昌天气预报气温日温差最大的时间是( )
A. 4 月 29 日B. 4 月 30 日C. 5 月 1 日D. 5 月 3 日
【题目】当今,人们对健康愈加重视,跑步锻炼成了人们的首要选择,许多与运动有关的手机APP应运而生,聪聪给自己定了目标,每天跑步![]() 公里.以目标路程为基准,超过的部分记为正,不足的部分记为负,他记下了七天的跑步路程:
公里.以目标路程为基准,超过的部分记为正,不足的部分记为负,他记下了七天的跑步路程:
日期 | 18日 | 19日 | 20日 | 21日 | 22日 | 23日 | 24日 |
路程(公里) | +1.72 | +3.20 | —1.91 | —0.96 | —1.88 | +3.30 | +0.07 |
(1)分别用含![]() 的代数式表示22日及23日的跑步路程;
的代数式表示22日及23日的跑步路程;
(2)如图所示是聪聪24日跑步路程是7.07公里,求![]() 的值;
的值;
(3)若跑步一公里消耗的热量为60千卡,请问聪聪跑步七天一共消耗了多少热量?