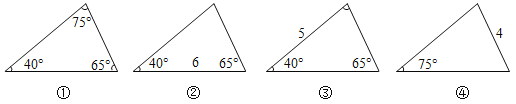ΧβΡΩΡΎ»ί
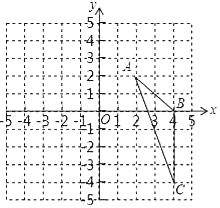
ΓΨΧβΡΩΓΩ»γΆΦ1Θ§≈ΉΈοœΏ![]() ”κx÷αΫΜ”ΎAΘ§BΝΫΒψΘ®ΒψA‘ΎΒψB”“≤ύΘ©Θ§”κy÷αΫΜ”ΎΒψCΘ§ΒψD «≈ΉΈοœΏΒΡΕΞΒψΘ°
”κx÷αΫΜ”ΎAΘ§BΝΫΒψΘ®ΒψA‘ΎΒψB”“≤ύΘ©Θ§”κy÷αΫΜ”ΎΒψCΘ§ΒψD «≈ΉΈοœΏΒΡΕΞΒψΘ°
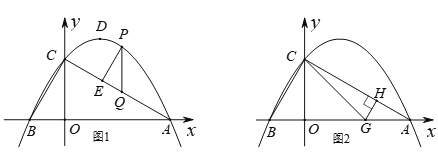
Θ®1Θ©»γΆΦ1Θ§Ν§Ϋ”ACΓΔBCΘ§»τΒψP «÷±œΏAC…œΖΫ≈ΉΈοœΏ…œ“ΜΕ·ΒψΘ§ΙΐΒψPΉςPE//BCΫΜ![]() ”ΎΒψEΘ§ΉςPQ//y÷αΫΜAC”ΎΒψQΘ§Β±ΓςPQE÷ή≥ΛΉν¥σ ±Θ§»τΒψM‘Ύy÷α…œΘ§ΒψN‘Ύx÷α…œΘ§«σPM+MN
”ΎΒψEΘ§ΉςPQ//y÷αΫΜAC”ΎΒψQΘ§Β±ΓςPQE÷ή≥ΛΉν¥σ ±Θ§»τΒψM‘Ύy÷α…œΘ§ΒψN‘Ύx÷α…œΘ§«σPM+MN![]() ANΒΡΉν–Γ÷ΒΘΜ
ANΒΡΉν–Γ÷ΒΘΜ
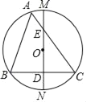
Θ®2Θ©»γΆΦ2Θ§ΒψGΈΣx÷α’ΐΑκ÷α…œ“ΜΒψΘ§«“OG=OCΘ§Ν§Ϋ”CGΘ§ΙΐΒψ![]() Ής
Ής![]() ”ΎΒψ
”ΎΒψ![]() Θ§ΫΪ
Θ§ΫΪ![]() »ΤΒψ
»ΤΒψ![]() Υ≥ ±’κ–ΐΉΣ
Υ≥ ±’κ–ΐΉΣ![]() Θ§Φ«–ΐΉΣ÷–ΒΡ
Θ§Φ«–ΐΉΣ÷–ΒΡ![]() ΈΣΓς
ΈΣΓς![]() Θ§‘Ύ–ΐΉΣΙΐ≥Χ÷–Θ§÷±œΏ
Θ§‘Ύ–ΐΉΣΙΐ≥Χ÷–Θ§÷±œΏ![]() Θ§
Θ§![]() Ζ÷±π”κ÷±œΏ
Ζ÷±π”κ÷±œΏ![]() ΫΜ”ΎΒψ
ΫΜ”ΎΒψ![]() Θ§
Θ§![]() Θ§Γς
Θ§Γς![]() ΡήΖώ≥…ΈΣΒ»―ϋ»ΐΫ«–ΈΘΩ»τΡή«κ÷±Ϋ”–¥≥ωΥυ”–¬ζΉψΧθΦΰΒΡ
ΡήΖώ≥…ΈΣΒ»―ϋ»ΐΫ«–ΈΘΩ»τΡή«κ÷±Ϋ”–¥≥ωΥυ”–¬ζΉψΧθΦΰΒΡ![]() ΒΡ÷ΒΘΜ»τ≤ΜΡήΘ§«κΥΒΟςάμ”…Θ°
ΒΡ÷ΒΘΜ»τ≤ΜΡήΘ§«κΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©PM+MN©¹![]() ANΒΡΉν–Γ÷Β «
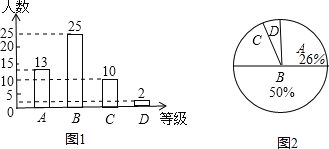
ANΒΡΉν–Γ÷Β «![]() ΘΜΘ®2Θ©¬ζΉψΧθΦΰΒΡ–ΐΉΣΫ«ΠΝΈΣ15ΓψΜρ37.5ΓψΜρ60ΓψΜρ127.5ΓψΘ°
ΘΜΘ®2Θ©¬ζΉψΧθΦΰΒΡ–ΐΉΣΫ«ΠΝΈΣ15ΓψΜρ37.5ΓψΜρ60ΓψΜρ127.5ΓψΘ°
ΓΨΫβΈωΓΩ
Θ®1Θ©ΙΙΫ®Εΰ¥ΈΚ· ΐΘ§«σ≥ωΒψPΉχ±ξΘ§»γΆΦ2÷–Θ§ΉςsinΓœOAF=![]() , ΉςPNΓΆAFΘ§‘ρ”–PM+MNΓίPNΘ§NH=
, ΉςPNΓΆAFΘ§‘ρ”–PM+MNΓίPNΘ§NH=![]() ANΘ§Ω…÷ΣPM+MN-AN
ANΘ§Ω…÷ΣPM+MN-AN![]() ANΒΡΉν–Γ÷ΒΦ¥ΈΣPHΒΡ≥ΛΘ§ΗυΨίΆ§Ϋ«ΒΡ»ΐΫ«Κ· ΐΩ…ΒΟPHΒΡ≥ΛΘΜ
ANΒΡΉν–Γ÷ΒΦ¥ΈΣPHΒΡ≥ΛΘ§ΗυΨίΆ§Ϋ«ΒΡ»ΐΫ«Κ· ΐΩ…ΒΟPHΒΡ≥ΛΘΜ
Θ®2Θ©Ζ÷ΥΡ÷÷«ι–ΈΖ÷±πΜ≠≥ωΆΦ–ΈΖ÷±π«σΫβΦ¥Ω…ΫβΨωΈ ΧβΘΜ
ΫβΘΚΘ®1Θ©»γΆΦ1Θ§Ε‘”Ύ≈ΉΈοœΏ![]() ,Ννy=0Θ§ΒΟΒΫx=6Μρ-2Θ§
,Ννy=0Θ§ΒΟΒΫx=6Μρ-2Θ§
ΓύAΘ®6Θ§0Θ©Θ§BΘ®-2Θ§0Θ©Θ§
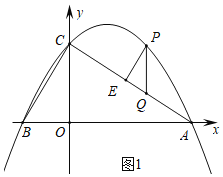
Β±x=0 ±Θ§y=2![]() ,
,
ΓύCΘ®0Θ§2![]() Θ©,
Θ©,
RtΓςAOC÷–Θ§OC=2![]() , OA=6,
, OA=6,
ΓύAC=4![]() ,
,
ΓύΓœACO=60ΓψΘ§Ά§άμΒΟΓœBCO=30Γψ
ΓύΓœACB=30Γψ+60Γψ=90ΓψΘ§
ÿPEøBCȧ
ΓύΓœPEQ=90ΓψΘ§
ΓΏPQΓΈy÷αΘ§
ΓύΓœACO=ΓœPQC=60ΓψΘ§
ΓύΒ±PQΉν¥σ ±Θ§ΓςPQE÷ή≥ΛΉν¥σΘ§
![]()
…η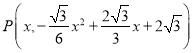 Θ§‘ρ
Θ§‘ρ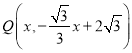 Θ§
Θ§
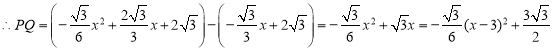
Β±x=3 ±Θ§PQΉν≥ΛΘ§¥Υ ±Θ§ΓςPQE÷ή≥ΛΉν¥σΘ§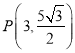
»γΆΦ2Θ§‘Ύy÷α…œ»ΓΒψ![]() Θ§ΒΟ
Θ§ΒΟ![]() Θ§
Θ§
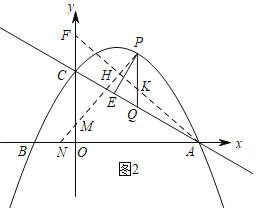
![]() Θ§ΉςPHΓΆAFΘ§ΫΜAF”ΎHΘ§ΫΜy÷α”ΎMΘ§ΫΜx÷α”ΎNΘ§AFΫΜPQ”ΎKΘ§
Θ§ΉςPHΓΆAFΘ§ΫΜAF”ΎHΘ§ΫΜy÷α”ΎMΘ§ΫΜx÷α”ΎNΘ§AFΫΜPQ”ΎKΘ§
![]()
![]()
‘ρPM+MN-AN![]() ANΒΡΉν–Γ÷ΒΦ¥ΈΣPHΒΡ≥ΛΘ§
ANΒΡΉν–Γ÷ΒΦ¥ΈΣPHΒΡ≥ΛΘ§
ΓΏAΘ®6Θ§0Θ©Θ§![]() Θ§
Θ§
“ΉΒΟ÷±œΏAFΒΡΫβΈω ΫΈΣ![]() Θ§
Θ§
Β±x=3 ±Θ§![]()
![]()
![]()
Ήέ…œΘ§PM+MN-AN![]() ANΒΡΉν–Γ÷Β «
ANΒΡΉν–Γ÷Β «![]() .
.
Θ®2Θ©»γΆΦ3÷–Θ§Β±MN=MGΓδ ±Θ§…ηOAΫΜGΓδN”ΎLΘ§
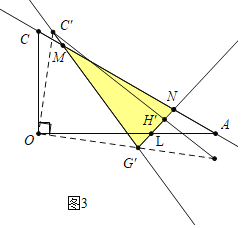
ΓΏΓœMGΓδN=75ΓψΘ§
ΓύΓœMNGΓδ=ΓœMGΓδN=75ΓψΘ§
ΓύΓœNLA=75Γψ-30Γψ=45ΓψΘ§
ΓΏΓœOLG'=ΓœNLA=45ΓψΘ§ΓœOGΓδL=45Γψ+75Γψ=120ΓψΘ§
ΓύΓœAOGΓδ=180Γψ-120Γψ-45Γψ=15ΓψΘ§
Γύ–ΐΉΣΫ«ΈΣ15ΓψΘ°
»γΆΦ4÷–Θ§Β±GΓδM=GΓδN ±Θ§…ηOAΫΜCΓδGΓδ”ΎLΘ°
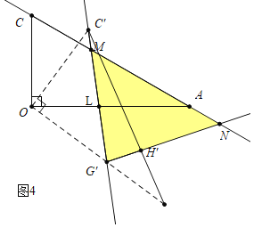
ΓΏΓœMGΓδN=75ΓψΘ§
ΓύΓœGΓδMN=![]() Θ®180Γψ-75ΓψΘ©=52.5ΓψΘ§
Θ®180Γψ-75ΓψΘ©=52.5ΓψΘ§
ΓύΓœOLGΓδ=ΓœALM=180Γψ-30Γψ-52.5Γψ=97.5ΓψΘ§
ΓύΓœAOGΓδ=180Γψ-97.5Γψ-45Γψ=37.5ΓψΘ§
Γύ–ΐΉΣΫ«ΈΣ37.5ΓψΘ°
»γΆΦ5÷–Θ§Β±NGΓδ=NM ±Θ§…ηOAΫΜGΓδCΓδ”ΎLΘ°

ΓΏΓœNGΓδM=ΓœNMGΓδ=75ΓψΘ§
ΓύΓœMNGΓδ=ΓœCAO=30ΓψΘ§
ΓύALΓΈNGΓδΘ§
ΓύΓœOLGΓδ=ΓœMG'N=75ΓψΘ§
ΓύΓœAOGΓδ=180Γψ-75Γψ-45Γψ=60ΓψΘ§
Γύ–ΐΉΣΫ«ΈΣ60ΓψΘ°
»γΆΦ6÷–Θ§Β±GΓδM=GΓδN ±Θ§
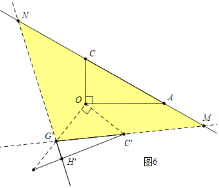
ΓΏΓœMGΓδN=180Γψ-75Γψ=105ΓψΘ§
ΓύΓœNMGΓδ=![]() Θ®180Γψ-105ΓψΘ©=37.5ΓψΘ§
Θ®180Γψ-105ΓψΘ©=37.5ΓψΘ§
ΓύΓœAOCΓδ=360Γψ-150Γψ-135Γψ-37.5Γψ=37.5ΓψΘ§
ΓύΓœAOGΓδ=90Γψ+37.5Γψ=127.5Γψ
Γύ–ΐΉΣΫ«ΈΣ127.5ΓψΘ°
Ήέ…œΥυ ωΘ§¬ζΉψΧθΦΰΒΡ–ΐΉΣΫ«ΠΝΈΣ15ΓψΜρ37.5ΓψΜρ60ΓψΜρ127.5ΓψΘ°

 ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ
ΧλΧλœρ…œ“Μ±ΨΚΟΨμœΒΝ–¥πΑΗ –Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗ
–Γ―ß…ζ10Ζ÷÷””Π”ΟΧβœΒΝ–¥πΑΗΓΨΧβΡΩΓΩ Ώ≤ΥΜυΒΊΈΣ―Γ≥ω ”Π –≥Γ–η«σΒΡΈςΚλ Ν―μΟγΘ§‘ΎΧθΦΰΜυ±ΨœύΆ§ΒΡ«ιΩωœ¬Θ§ΫΪΦΉΓΔ““ΝΫΗωΤΖ÷÷ΒΡΈςΚλ Ν―μΟγΗς500÷ξ÷÷÷≤‘ΎΆ§“ΜΗω¥σ≈οΘ°Ε‘ –≥ΓΉνΈΣΙΊΉΔΒΡ≤ζΝΩΫχ––ΝΥ≥ι―υΒς≤ιΘ§ΥφΜζ¥”ΦΉΓΔ““ΝΫΗωΤΖ÷÷ΒΡΈςΚλ Ν―μΟγ÷–Ης ’Φ·ΝΥ50÷ξ―μΟγ…œΒΡΙ“Ιϊ ΐΘ®ΈςΚλ ΝΒΡΗω ΐΘ©Θ§≤ΔΕ‘ ΐΨίΘ®Ηω ΐΘ©Ϋχ––’ϊάμΓΔΟη ωΚΆΖ÷ΈωΘ§œ¬ΟφΗχ≥ωΝΥ≤ΩΖ÷–≈œΔ.
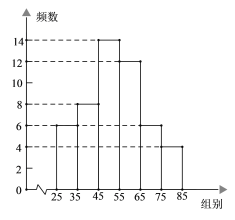
a. ΦΉΤΖ÷÷Ι“Ιϊ ΐΤΒ ΐΖ÷≤Φ÷±ΖΫΆΦΘ® ΐΨίΖ÷≥…6ΉιΘΚ25Γήx<35Θ§35Γήx<45Θ§45Γήx<55Θ§55Γήx<65Θ§65Γήx<75Θ§75Γήx<85Θ©.
b. ΦΉΤΖ÷÷Ι“Ιϊ ΐ‘Ύ45Γήx<55’β“ΜΉιΒΡ «ΘΚ
45Θ§45Θ§46Θ§47Θ§47Θ§49Θ§49Θ§49Θ§49Θ§50Θ§50Θ§51Θ§51Θ§54
c. ΦΉΓΔ““ΤΖ÷÷Ι“Ιϊ ΐΒΡΤΫΨυ ΐΓΔ÷–ΈΜ ΐΓΔ÷Ύ ΐ»γœ¬ΘΚ
ΤΖ÷÷ | ΤΫΨυ ΐ | ÷–ΈΜ ΐ | ÷Ύ ΐ | ΖΫ≤ν |
ΦΉ | 49.4 | m | 49 | 1944.2 |
““ | 48.6 | 48.5 | 47 | 3047 |
ΗυΨί“‘…œ–≈œΔΘ§ΜΊ¥πœ¬Ν–Έ Χβ:
(1)±μ÷–m= ΘΜ
(2) ‘ΙάΦΤΦΉΤΖ÷÷Ι“Ιϊ ΐ≥§Ιΐ49ΗωΒΡΈςΚλ Ν―μΟγΒΡ ΐΝΩΘΜ
(3)Ω…“‘ΆΤΕœ≥ω ΤΖ÷÷ΒΡΈςΚλ Ν―μΟγΗϋ ”Π –≥Γ–η«σΘ§άμ”…ΈΣ Θ®÷Ν…Ό¥”ΝΫΗω≤ΜΆ§ΒΡΫ«Ε»ΥΒΟςΆΤΕœΒΡΚœάμ–‘Θ©.
ΓΨΧβΡΩΓΩΡ≥–Θ–Υ»Λ–ΓΉιΨΆΓΑΉνœκ»ΞΒΡ’Ρ÷ί5ΗωΉνΟάœγ¥εΓ±ΥφΜζΒς≤ιΝΥ±Ψ–Θ≤ΩΖ÷―ß…ζ. “Σ«σΟΩΈΜΆ§―ß―Γ‘ώ«“÷ΜΡή―Γ‘ώ“ΜΗωΉνœκ»ΞΒΡΉνΟάœγ¥ε. œ¬Οφ «ΗυΨίΒς≤ιΫαΙϊΜφ÷Τ≥ωΒΡ…–≤ΜΆξ’ϊΆ≥ΦΤ±μΚΆΆ≥ΦΤΆΦΘ§Τδ÷–xΓΔy «¬ζΉψx<yΒΡ’ΐ’ϊ ΐ.
ΉνΟάœγ¥ε“βœρΆ≥ΦΤ±μ
ΉνΟάœγ¥ε | »Υ ΐ |
AΘΚΝζΚΘήΛΟά¥ε | 10 |
BΘΚΜΣΑ≤ΙΌ°¨¥ε | 11 |
CΘΚ≥ΛΧ©…Ϋ÷Ί¥ε | 4x |
DΘΚΡœΨΗΥΰœ¬¥ε | 9 |
EΘΚΕΪ…ΫΑΡΫ«¥ε | 3y |
ΉνΟάœγ¥ε“βœρ…»–ΈΆ≥ΦΤΆΦ
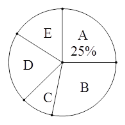
ΗυΨί“‘…œ–≈œΔΘ§Ϋβ¥πœ¬Ν–Έ ΧβΘΚ
(1)«σxΓΔyΒΡ÷ΒΘΜ
(2)»τΗΟ–Θ”–1200Οϊ―ß…ζΘ§«κΙάΦΤΓΑΉνœκ»ΞΜΣΑ≤ΙΌ°¨¥εΓ±ΒΡ―ß…ζ»Υ ΐ.