题目内容
【题目】在平面直角坐标系中,函数y=ax2﹣2ax﹣4a(x≥0)的图象记为M1,函数y=﹣ax2﹣2ax+4a(x<0)的图象记为M2,其中a为常数,且a≠0,图象M1,M2合起来得到的图象记为M.
(1)当图象M1的最低点到x轴距离为3时,求a的值.
(2)当a=1时,若点(m,![]() )在图象M上,求m的值,
)在图象M上,求m的值,
(3)点P、Q的坐标分别为(﹣5,﹣1),(4,﹣1),连结PQ.直接写出线段PQ与图象M恰有3个交点时a的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() 或a=
或a=![]() .
.
【解析】
(1)因为提到“最低点”,所以函数图象M1对应的抛物线开口向上,a>0,令顶点纵坐标=3即求出a的值.
(2)把点在图象M1或图象M2进行分类讨论,把a=1和y=![]() 代入解析式即求出m的值.
代入解析式即求出m的值.
(3)把a>0时图象M的大致草图画出,根据图象观察和计算说明线段PQ所在位置对交点个数的影响,得到a的范围,同理可计算a<0时的情况.
解:(1)∵y=ax22ax4a=a(x1)25a,且图象M1的最低点到x轴距离为3
∴a>0,
∴|5a|=3,即5a=3
∴a=![]() ;
;
(2)当a=1时,点(m,![]() )在图象M上,
)在图象M上,
①若点在图象M1上,即m≥0,m22m4=![]() ,
,
解得:m1=![]() ,m2=
,m2=![]() (舍去);
(舍去);
②若点在图象M2上,即m<0,m22m+4=![]() ,
,
解得:m3=![]() (舍去),m4=
(舍去),m4=![]() ,
,
综上所述,m的值为![]() 或
或![]() ;
;
(3)若a>0,则图象M的大致形状如图1,
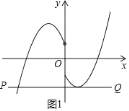
若线段PQ经过图象M1的顶点(1,5a)
则5a=1,得a=![]() ,
,
对于图象M2,![]() 时,
时,
解得:![]() (舍去),
(舍去),![]() ,
,
∵![]() ,
,
∴直线PQ与图象M2的交点在点P的右侧
∴线段PQ与图象M2有一个交点,与M有两个交点,
而M1与y轴的交点为(0,-4a),
∴当5a<-1≤-4a时,线段PQ与图象M有三个交点,
解得:![]() ;
;
同理当a<0时,

同理可得![]() ,而当a=
,而当a=![]() 即上图情况是,线段PQ的交点恰好为Q点,此时有三个交点,而
即上图情况是,线段PQ的交点恰好为Q点,此时有三个交点,而![]() 时,图像线段PQ的交点只有个,右侧没有交点,所以a=
时,图像线段PQ的交点只有个,右侧没有交点,所以a=![]() ,
,
故线段PQ与图象M恰有3个交点时a的取值范围是:![]() 或a=
或a=![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
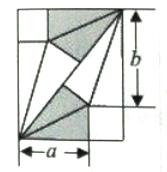
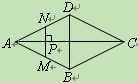
小学生10分钟应用题系列答案【题目】如图,点P是菱形ABCD的对角线AC上的一个动点,过点P垂直于AC的直
线交菱形ABCD的边于M、N两点.设AC=2,BD=1,AP=x,△AMN的面积为y,则
y关于x的函数图象大致形状是【 】

【题目】蔬菜基地为选出适应市场需求的西红柿秧苗,在条件基本相同的情况下,将甲、乙两个品种的西红柿秧苗各500株种植在同一个大棚.对市场最为关注的产量进行了抽样调查,随机从甲、乙两个品种的西红柿秧苗中各收集了50株秧苗上的挂果数(西红柿的个数),并对数据(个数)进行整理、描述和分析,下面给出了部分信息.
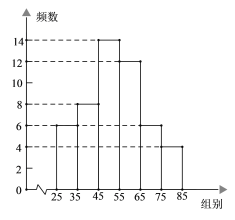
a. 甲品种挂果数频数分布直方图(数据分成6组:25≤x<35,35≤x<45,45≤x<55,55≤x<65,65≤x<75,75≤x<85).
b. 甲品种挂果数在45≤x<55这一组的是:
45,45,46,47,47,49,49,49,49,50,50,51,51,54
c. 甲、乙品种挂果数的平均数、中位数、众数如下:
品种 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 49.4 | m | 49 | 1944.2 |
乙 | 48.6 | 48.5 | 47 | 3047 |
根据以上信息,回答下列问题:
(1)表中m= ;
(2)试估计甲品种挂果数超过49个的西红柿秧苗的数量;
(3)可以推断出 品种的西红柿秧苗更适应市场需求,理由为 (至少从两个不同的角度说明推断的合理性).
【题目】某校的一个社会实践小组对本校学生中开展主题为“垃圾分类知多少”的专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,划分等级后的数据整理如下表:
等级 | 非常了解 | 比较了解 | 基本了解 | 不太了解 |
频数 | 20 | 35 | 41 | 4 |
(1)请根据调查结果,若该校有学生![]() 人,请估计这些学生中“比较了解”垃圾分类知识的人数.
人,请估计这些学生中“比较了解”垃圾分类知识的人数.
(2)在“比较了解”的调查结果里,其中九(1)班学生共有![]() 人,其中
人,其中![]() 名男生和
名男生和![]() 名女生,在这
名女生,在这![]() 人中,打算随机选出
人中,打算随机选出![]() 位进行采访,求出所选两位同学恰好是1名男生和1名女生的概率.(要求列表或画树状图)
位进行采访,求出所选两位同学恰好是1名男生和1名女生的概率.(要求列表或画树状图)