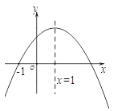题目内容
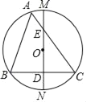
【题目】已知:正方形ABCD中,∠MAN=45°,∠MAN绕点A顺时针旋转,它的两边分别交CB、DC(或它们的延长线)于点M、N.
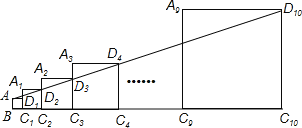
(1)当∠MAN绕点A旋转到BM=DN时(如图1),请你直接写出BM、DN和MN的数量关系:__________.
(2)当∠MAN绕点A旋转到BM≠DN时(如图2),(1)中的结论是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明.
(3)当∠MAN绕点A旋转到如图3的位置时,线段BM、DN和MN之间又有怎样的数量关系?请写出直接写出结论.

【答案】(1)BM+DN=MN.(2)成立,理由见解析; (3)DN﹣BM=MN.
【解析】分析:
(1)如图4,把△AND绕点A顺时针旋转90°得到△ABF,则由已知可得点C、B、F三点共线,结合旋转的性质可得MF=BM+BF=BM+DN,再证△AMN≌△AMF即可得到所求结论;
(2)如图5,把△AND绕点A顺时针旋转90°得到△ABE,与(1)同理可得MN=DN+BM;
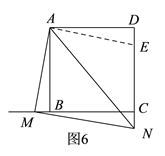
(3)如图6,在DC是截取DE=BM,连接AE,先证△ADE≌△ABM,再证△AMN≌△AEN即可证得DN-BM=MN.
详解:
(1)BM+DN=MN. 理由如下:
如图4,把△AND绕点A顺时针旋转90°得到△ABF,则由题意可得:点C、B、F三点共线,
∴由旋转的性质可得:BF=DN,AF=AN,∠BAF=∠DAN,
∵∠BAD=90°,∠MAN=45°,
∴∠BAM+∠DAN=45°,
∴∠BAF+∠BAM=45°=∠MAF=∠MAN,
又∵AM=AM,
∴△AMF≌△AMN,
∴MF=MN,
又∵MF=BM+BF,BF=DN,
∴MN=BM+DN;

(2)成立,理由如下:
如图5,把△ADN绕点A顺时针旋转90°,得到△ABE,则可得E、B、M三点共线.
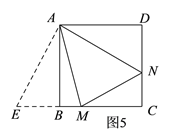
∴∠EAM=90°﹣∠NAM=90°﹣45°=45°,AE=AN,BE=DN,
又∵∠NAM=45°,
∴∠EAM=∠NAM,
∴在△AEM与△ANM中,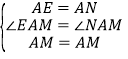 ,
,
∴△AEM≌△ANM(SAS),
∴ME=MN,
∵ME=BE+BM=DN+BM,
∴DN+BM=MN;
(3)DN-BM=MN.理由如下:
如图6,在DC上截取DE=BM,连接AE,
∵∠ADE=∠ABM=90°,AD=AB,
∴△ADE≌△ABM,
∴AE=AM,∠DAE=∠BAM,
∵∠BAM+∠BAN=∠MAN=45°,
∴∠DAE+∠BAN=45°,
∴∠EAN=90°-∠DAE-∠BAN=45°=∠MAN,
又∵AN=AN,
∴△EAN≌△MAN,
∴EN=MN,
又∵DN-DE=EN,
∴DN-BM=MN.

【题目】如图,点P是菱形ABCD的对角线AC上的一个动点,过点P垂直于AC的直
线交菱形ABCD的边于M、N两点.设AC=2,BD=1,AP=x,△AMN的面积为y,则
y关于x的函数图象大致形状是【 】

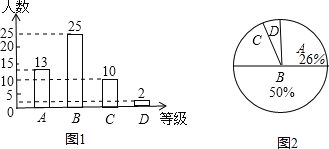
【题目】蔬菜基地为选出适应市场需求的西红柿秧苗,在条件基本相同的情况下,将甲、乙两个品种的西红柿秧苗各500株种植在同一个大棚.对市场最为关注的产量进行了抽样调查,随机从甲、乙两个品种的西红柿秧苗中各收集了50株秧苗上的挂果数(西红柿的个数),并对数据(个数)进行整理、描述和分析,下面给出了部分信息.
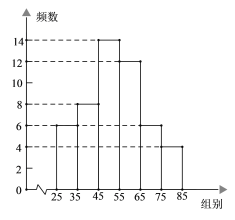
a. 甲品种挂果数频数分布直方图(数据分成6组:25≤x<35,35≤x<45,45≤x<55,55≤x<65,65≤x<75,75≤x<85).
b. 甲品种挂果数在45≤x<55这一组的是:
45,45,46,47,47,49,49,49,49,50,50,51,51,54
c. 甲、乙品种挂果数的平均数、中位数、众数如下:
品种 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 49.4 | m | 49 | 1944.2 |
乙 | 48.6 | 48.5 | 47 | 3047 |
根据以上信息,回答下列问题:
(1)表中m= ;
(2)试估计甲品种挂果数超过49个的西红柿秧苗的数量;
(3)可以推断出 品种的西红柿秧苗更适应市场需求,理由为 (至少从两个不同的角度说明推断的合理性).